http://www3.gmu.edu/departments/economics/bcaplan
Econ 345
Fall, 1998
Weeks 1-2: Brief Review of Basic Statistics
- What is Econometrics?
- Econometrics is the application of statistics to economics.
- Econometrics uses computers to apply statistics to economic questions.
- Contrast with economic history.
- Qualified skepticism about the usefulness of econometrics.
- Probability
- Where x is any event,
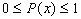 . The probability of an event ranges between impossible and certain.
. The probability of an event ranges between impossible and certain.
- Where X is the set of all possible events x,
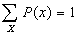 . The probability that some possible event or other occurs is certain.
. The probability that some possible event or other occurs is certain.
- Graphing discrete probability densities; graphing continuous probability densities.
- Independence: X and Y are independent iff P(X,Y)=P(X)P(Y).
- Conditional probability: P(X|Y)=P(X,Y)/P(Y).
- Expected Values
- E(X) is just the mean or "average" of a random variable X. Formally,
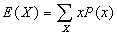 .
.
- Note:
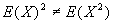
unless X is a constant.
- Variance and Standard Deviation
- Var(X)
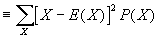 . SD(X) is equal to the square root of Var(X). Intuitively, both measure the "spread" of a distribution. If X is a constant, then both SD(X) and Var(X)=0.
. SD(X) is equal to the square root of Var(X). Intuitively, both measure the "spread" of a distribution. If X is a constant, then both SD(X) and Var(X)=0.
- In practice, Var(X) is a pain to calculate using the above definition. Fortunately, there is extremely useful formula that permits ready calculation:
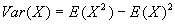 .
.
- Summing
N independent draws from a random variable X has a very interesting property: while the expectation of the average of N draws is simply E(X), the SD(average of N independent draws of X)=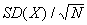
. Intuitively, this means that the more independent draws, the more accurate the estimate of E(X) becomes.
- Covariance and Correlation
- Both covariance and correlation measure the linear association of two variables: if covariance and correlation for two variables is positive, the two variables are positively associated; if negative, then the two variables are negatively associated. If random variables are independent, then their covariance and correlation is zero.
- Cov(X,Y)
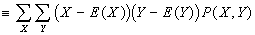 ; slightly simpler formula: Cov(X,Y)=E(XY)-E(X)E(Y). Covariance ranges over the real numbers.
; slightly simpler formula: Cov(X,Y)=E(XY)-E(X)E(Y). Covariance ranges over the real numbers.
- Corr(X,Y)
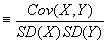 . The correlation coefficient ranges between -1 and +1; this makes it much easier to interpret than covariance. If
. The correlation coefficient ranges between -1 and +1; this makes it much easier to interpret than covariance. If 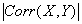
is high, then it is possible to make good predictions about one variable if you know the other.
- Estimating Population Mean and Population Variance
- If you observe all members of a population, then it is straightforward to calculate the mean and the variance. However, in many cases we observe only PART of the population - and then use what we have seen to estimate what the whole population is like.
- An easy case: estimating the population mean by simply taking the sample mean.
- Tougher case: estimating the population variance using:
 .
.
- Why do you divide by (n-1) instead of n? Think about the variance of a single point.
- Notice that we could have just used ONE observation instead of the sample mean. But that is a bad idea because using more data gives us a lower variance for our estimate. Intuition: remember that the Var(average of N independent draws of X)=
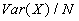
.
- Standard errors, Confidence Intervals, and Hypothesis Testing
- Terminological note:
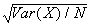 is often called the "standard error" of an estimate.
is often called the "standard error" of an estimate.
- Important fact
: a sample average of observations from a population less its true mean divided by its standard error has a t-distribution with (n-1) degrees of freedom. In math, 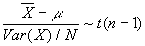 .
.
- The t-distribution looks very similar to the more familiar Normal distribution, but you need to use it when Var(X) is estimated rather than known. When n is large, the t-distribution becomes approximately Normal.
- You can use the above formula to construct a Confidence Interval, or range within which the true value of something lies with a certain probability. For example, suppose that we observe 61 dogs' weights, and find that the sample mean is 40 pounds and the sample variance is 15 pounds. Then to construct a 95% Confidence Interval:
- Plug in the numbers. The sample mean is 40. The sample variance is 15 pounds, so with 61 observations, the standard error is
 . 61-1=60, so we must use the t(60) distribution.
. 61-1=60, so we must use the t(60) distribution.
- Now, go to the t-distribution table. The table shows the values for the right tail, so the extreme left and right tails combined have double the value of the right tail alone.
- This means that for a 95% C.I., we want the .025 (2.5%) column. For the t(60) distribution, go to the row marked 60.
- Get the value at the given row and column. It is 2.000.
- Multiply this number by the standard error - in this case, .496, to get .992.
- The 95% C.I. here is therefore 40±.992.
- Hypothesis testing is trivial once you understand C.I.'s.
- Just plug your hypothesis into the C.I. instead of the sample mean, and see if your observed sample mean lies within the C.I.
- If your sample mean lies outside the C.I., you "reject the hypothesis." Otherwise you can accept it (or as some prefer to say, "fail to reject it").
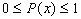 . The probability of an event ranges between impossible and certain.
. The probability of an event ranges between impossible and certain.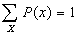 . The probability that some possible event or other occurs is certain.
. The probability that some possible event or other occurs is certain.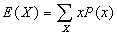 .
. 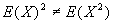
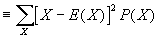 . SD(X) is equal to the square root of Var(X). Intuitively, both measure the "spread" of a distribution. If X is a constant, then both SD(X) and Var(X)=0.
. SD(X) is equal to the square root of Var(X). Intuitively, both measure the "spread" of a distribution. If X is a constant, then both SD(X) and Var(X)=0.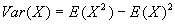 .
.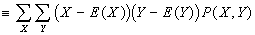 ; slightly simpler formula: Cov(X,Y)=E(XY)-E(X)E(Y). Covariance ranges over the real numbers.
; slightly simpler formula: Cov(X,Y)=E(XY)-E(X)E(Y). Covariance ranges over the real numbers.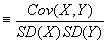 . The correlation coefficient ranges between -1 and +1; this makes it much easier to interpret than covariance. If
. The correlation coefficient ranges between -1 and +1; this makes it much easier to interpret than covariance. If 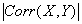
 .
.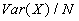
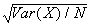 is often called the "standard error" of an estimate.
is often called the "standard error" of an estimate. . 61-1=60, so we must use the t(60) distribution.
. 61-1=60, so we must use the t(60) distribution.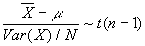 .
.