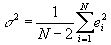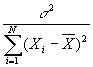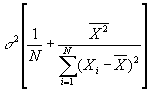http://www3.gmu.edu/departments/economics/bcaplan
Econ 345
Fall, 1998
Weeks 3-4: Regression with One Variable
- Curve-fitting
- Given a scatter of points, how can you "fit" a single equation to describe it?
- With three or more points, it will normally be impossible to fit it exactly.
- It is possible to draw numerous lines through a bunch of points, but which is the "best" line describing the behavior of the data?
- General answer: minimize some function of the errors.
- Least-Squares Estimator
- Most common answer (which will be used throughout this class): minimize sum of squared errors. Aka "least-squares estimator."
- Step 1: Assume data fits some equation of general form: Yi= a + bXi +ei, where Y is the dependent variable, X is the independent variable, a and b are constants, and e is an error term that ensures that the equation is true.
- Step 2: Define SSE, the "sum of squared errors."
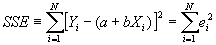
- Step 3: minimize SSE, and solve for a and b. Then you will know what values of a and b minimize SSE given Y and X.
- Derivation of the Slope and Intercept Terms
- Standard minimization technique: take the partial derivatives wrt the variables you are minimizing over:
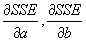 , and set the equation equal to 0.
, and set the equation equal to 0.
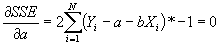
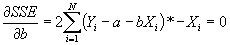
- Simplifying:
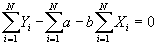
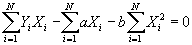
- Multiplying by 1/N and simplying, the first equation becomes:
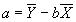 .
.
- Substitute value for a into second equation, to get:
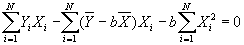
- Solving for b:
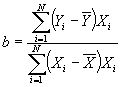
- Useful formula:
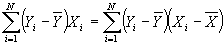
- Now define
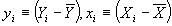 . Then we have another, more convenient formula for b:
. Then we have another, more convenient formula for b: 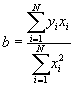
- Important Properties of The Simple Regression Model
- Property #1: Residuals sum to zero.
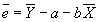 ; plug in for a to get
; plug in for a to get 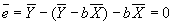 .
.
- Property #2: Actual and predicted values of Y have the same mean.
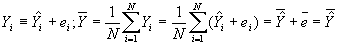
- Property #3: Least squares residuals are uncorrelated with the independent variable. Recall that if the correlation between two variables is zero, then the covariance between them is also zero. Then this may be proved using the following (and subbing in for b):
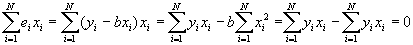
- Property #4: Predicted values of Y uncorrelated with least squares residual. Again, this will be proved by showing that the covariance =0.
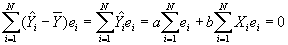
- R2
- Define

- TSS=RSS+SSE
- R2=1-SSE/TSS
- This gives an interesting measure of how much of the variation in the data has been "explained." R2 ranges between 0 and 1.
- Derivation of the Standard Errors for Slope and Intercept
- It turns out to be important to estimate the variance of the error terms. This can be done using a simple formula:
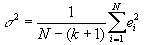 , where k is the number of independent variables (not counting the constant). With only 1 independent variable, this formula becomes:
, where k is the number of independent variables (not counting the constant). With only 1 independent variable, this formula becomes: 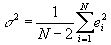
- Now this can be used to estimate the variance of b:
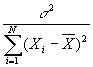
- As well as the variance of a:
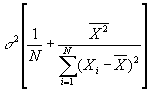
- Knowing these is important: it lets us know how precise our estimate is.
- Correlation vs. Causation
- After doing all of this math, it is very easy to overestimate how far we have actually gotten.
- We can describe the correlation between variables, but does this show that one thing is causing the other? Could there be third factors causing both?
- Examples:
- Russian doctors
- Police and crime
- Price of eggs and price of chickens
- Others?
- Bottom line: You have to be very careful when you interpret regression equations, especially when you havenít gotten your data from double-blind random sampling.
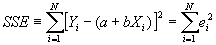
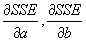 , and set the equation equal to 0.
, and set the equation equal to 0.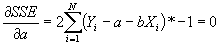
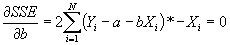
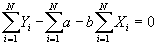
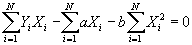
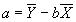 .
.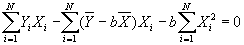
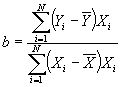
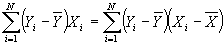
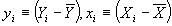 . Then we have another, more convenient formula for b:
. Then we have another, more convenient formula for b: 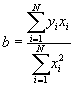
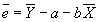 ; plug in for a to get
; plug in for a to get 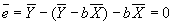 .
.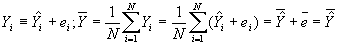
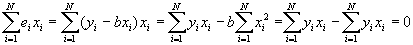
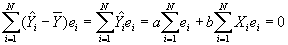

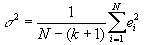 , where k is the number of independent variables (not counting the constant). With only 1 independent variable, this formula becomes:
, where k is the number of independent variables (not counting the constant). With only 1 independent variable, this formula becomes: