http://www3.gmu.edu/departments/economics/bcaplan
Econ 345
Fall, 1998
Week 5: Choice of Functional Forms (+some computing)
- Doing Regression Using Eviews
- Open your Eviews workfile.
- Go to the (lower) "Objects" heading. Select "New Object."
- An input box now appears. Select the option "Equation."
- Now simply follow the instructions in the next input box that appears. The easiest thing to do is just type your dependent variable, followed by a full list of your independent variables (don't forget to put a "c" if you want a constant!).
- A screen with output for the regression equation you estimated will pop up. You have now created an Equation object; give it a name.
- There are several options you can combine with an Equation object. We'll discuss them as needed. First just get used to plain vanilla use of Equations.
- Doing Linear Changes to a Regression Specification
- The standard regression model is written
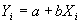 . Notice that this model is linear. It remains linear if you add more independent variables, each with its own coefficient.
. Notice that this model is linear. It remains linear if you add more independent variables, each with its own coefficient.
- What happens to your estimate of b if you DOUBLE all values of X? You might do this if you changed from English to metric units of something. Or maybe you prefer to switch from writing your number in 1000's to writing it in 1,000,000's.
- Answer: The coefficient changes so that the prediction remains unchanged. If you switch from inches to feet (you divide all measurements by 12), then your coefficient increases by a factor of 12.
- What happens to your estimates of a and b if you DOUBLE all values of Y?
- a
and b also double.
- What happens if you ADD the same number to all of the X's? For example, if you decide to replace "years of college" with "years of education"?
- Answer: b won't change. Instead, if you add c to every value of X, the constant falls by b*c.
- What happens if you ADD the same number to all of the Y's?
- Answer: b won't change. Instead, if you add c to every value of Y, the constant rises by c.
- Summing up: Linear rescaling - whether by subtracting a constant from a variable, or multiplying a variable by a constant, does nothing to change the prediction.
- Double-check this using Eviews: Go to the "Genr" heading to define a new variable equal to 2*inflation. Then run regressions on both versions and see if you get the same answer.
- Doing Non-Linear Changes to a Specification
- Relations are often non-linear. Ex: Price increases under hyper-inflation. (Hall, p. 74)
- But it is possible to handle non-linear operations within the linear regression model! Just replace
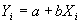 with
with 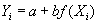 or
or  , and estimate the new regression.
, and estimate the new regression.
- Non-linear operations won't leave coefficients the same. Coefficients won't be linear functions of old coefficients, either.
- You can also include both a linear and a non-linear measurement of the same variable in one regression equation. Example: Common to regress earnings on Experience and Experience2 since the data show a gradual flattening of the return to education.
- Taking Logs of a Variable
- Eviews command: Under Genr, do lprice=log(price).
- When might you want to do this?
- If your variable shows exponential growth.
- Ex: prices during a hyperinflation.
- If your variable has a big right tail.
- Ex: the distribution of income.
- Squaring a Variable
- Eviews command: under Genr, do usq=un^2
- When might you want to do this?
- If you variable rises at a decreasing rate (eventually the slope gets flatter).
- Ex: The effect of more years of experience
- If you expect a non-linear response.
- Ex: Demand for air conditioners may rise more than linearly. 1 person buys air conditioners because average temperature rises .1 degrees, but 10,000 people buy them because it rises 10 degrees.
- Taking First Differences
- Subtract Xt-1 from Xt. (It's called "first difference" because you take the difference of a variable and its first lag).
- Hummer command: if you have a single time series, do Genr, then INFFD=INF-INF(-1).
- Suppose that you observe me every year. Last year, you observed that I had 20 years of education and $10,000 in income. This year I have 21 years of education and $40,000 income. The first difference way of writing this is to say that YFD=+1, and IFD=$30,000.
- Notice that this is NOT a linear transformation. I don't subtract a constant from each measure of X. I subtract a different number from each X.
- When do you want to do this?
- When you are worried that you have a spurious correlation.
- Ex: More educated people make more money, but does changing the education of a given person make that person make more money?
- If your theory predicts an effect of changes rather than levels.
- Ex: Some theories predict that the level of inflation makes no difference, but changes in the level of inflation make a difference.
- Taking Percentage Changes
- Hummer command: Genr INFPER=(INF/INF(-1)-1)*100
- When would you want to do this?
- If a variable is constantly increasing, like many time series.
- Ex: Comparing percent change in money to the inflation rate.
- Ex: Comparing percent change in real GDP with percent change in nominal GDP.
- If it makes the results easier to interpret.
- Ex: What is the percent change in a professor's number of books per year?
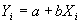 . Notice that this model is linear. It remains linear if you add more independent variables, each with its own coefficient.
. Notice that this model is linear. It remains linear if you add more independent variables, each with its own coefficient.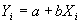 with
with 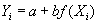 or
or  , and estimate the new regression.
, and estimate the new regression.