Prof. Bryan Caplan
Econ 345
bcaplan@gmu.edu
http://www3.gmu.edu/departments/economics/bcaplan
Econ 345
Fall, 1998
Week 13: Simple Econometrics and the Random Walk Hypothesis
- Astrology and Financial Markets
- There are innumerable highly paid experts on financial markets who claim to have special insight into the future.
- Technical analysts try to extrapolate trends, etc.
- Fundamental analysts try to find "under-valued" and "over-valued" companies, based on e.g. price/earnings ratios.
- Digression: The present value of $1 t years from now is:
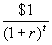 . This is how much money you would have to put in the bank today to have $1 t years from now.
. This is how much money you would have to put in the bank today to have $1 t years from now.
- What is the relationship between PDV and price/earnings ratio? It is fairly close: as interest rates decline, PDV increases, and so does the price/earnings ratio.
- Astrology funds claim to use astrology to select winning stocks.
- Question: Who (if anyone) knows what they are talking about?
- Question: If anyone knows what they are talking about, then how do all of the other advisors using wrong theories survive?
- Darts, Monkeys, Chickens, and the S&P - More Puzzles
- Economists interested in these questions tried comparing the performance of expert fund managers with the results of randomly selecting stocks.
- In general, they found that the randomly selected stocks did as well as - or better than! - the "experts."
- "Monkeys throwing darts at the financial times beat half of the 'experts.'"
- The chicken against the experts.
- The S&P 500 is a popular index of 500 stocks. Again, economists noticed that half or more of the experts lost to the S&P.
- The Random Walk Hypothesis: An Informal Statement
- How is all this possible?
- Millions of people are desperately searching for any information relevant to financial markets. As soon as the information arrives, they rush to buy or sell.
- But if enough people are rushing to buy or sell - only the very quickest people actually benefit from the new information. By the time you pick up the phone to call your broker, the price has already fully incorporated the new information.
- Implication: Price changes are unpredictable. Only news in the literal sense of new, unexpected information will affect prices in financial markets.
- Suppose for example that next quarter a firm is going to earn high profits. If this information becomes available now, the price will rise immediately, not a quarter from now.
- The better financial journalists recognized this in statements like: "The price went up because the losses were not as bad as expected."
- The Random Walk Hypothesis: A Formal Statement
- The random walk hypothesis says that the price change is random, not the price:
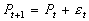 , where epsilon is an independently drawn random variable.
, where epsilon is an independently drawn random variable.
- Epsilon is often assumed to have a mean of zero; if it has a positive mean, this means that the price tends to rise over time.
- Normal distribution of epsilon often assumed.
- If the random walk hypothesis is true, and if epsilon has a mean of zero, then the best guess of tomorrow's price is simply today's price:
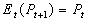 .
.
- Past changes in the price will not predict future changes in price; neither will any other past information predict changes in price.
- Testing the Random Walk: 3 Data Sets
- When would the Random Walk hypothesis apply?
- Market-clearing. If there's rationing or sticky prices, you would not expect the random walk to work.
- Cheap storage. If strawberries rot quickly or cost a lot to store, you would not necessarily buy them today even though you know they'll be more expensive tomorrow.
- Most plausible candidates for Random Walk hypothesis:
- Stocks
- Bonds
- Commodity futures
- Commodities
- I had my R.A. pick three variables at random. They are as follows:
- Monthly index of 500 stocks, 1945/1-1995/12.
- Yearly closing price of gold, 1970-1996
- Monthly spot price of cotton, 1948/1-1995/11.
- The random walk hypothesis makes the strong claim that no past information will predict current price changes. We'll limit our "past information" to past prices of the variable. In other words, we'll see if it is possible to predict the changes of a variable from its lags.
- The Random Walk: Evidence from Stock Index Data
- The random walk is consistent with a positive price trend (then the random variable just has a positive mean, but is still independently distributed).
- Regression #1: Regress % change in monthly price on 1st lag.
- Result: Appears unfavorable to Random Walk hypothesis: if the return last month was 1% higher, you can expect this month's return to be .24% greater. Highly significant correlation; however, note the low R2: you can't make a very good prediction using this info, even though it's highly significant - as R.W. would suggest. (Also note: We've got a lot of data, so high t-stats are less surprising!)
- Regression #2: Regression % change in monthly price on 6 lags.
- Result: 1st lag remains highly significant, although none of the other 5 lags are. Note that the R2 remains very low.
- Regression #3: Convert monthly data to annual. Then regress % change in annual price on 1st lag.
- First lag is not significantly different from zero. Consistent with Random Walk.
- Regression #4: Still using annualized data: Regression % change in annual price on 4 lags.
- Result: First 3 lags are insignificant; 4th lag is significant. Overall reasonably consistent with Random Walk.
- The Random Walk: Evidence from Gold Prices
- Before 1970, the gold price was pegged by the government, so predicting it isn't very interesting. We use the annual data for 1970-1996 to test the RWH.
- Regression #5: Regress % ch in gold price on first lag.
- Result: First lag is insignificant. Consistent with RWH.
- Regression #6: Regression % ch in gold price on 4 lags.
- Result: All four lags are insignificant. Consistent with RWH.
- The Random Walk: Evidence from Cotton Prices
- Use monthly data for price of cotton for 1948/1 to 1995/11. Note that due to e.g. storage costs we might expect RWH to fail. (Futures price of cotton would be a better candidate). But we'll try it anyway.
- Regression #7: Regress % change in monthly cotton price on 1st lag.
- Result: Significant positive impact (although note very low R2!).
- Regression #8: Regress % change in monthly cotton price on 6 lags.
- Result: Lags #1 to #3 are all significant (although #2 is negative!). R2 remains very low. But overall hard to reconcile with RWH.
- Regression #9: Annualize cotton price data. Then regress % change in annual price on 1st lag.
- Result: 1st lag not significant. Consistent with RWH.
- Regression #10: Regress % change in annual price on 4 lags.
- Result: All 4 lags are insignificant.
- Overall Conclusions
- Limitations: Note that we merely picked three variables, and only used past values of e.g. gold to explain the current price of gold. Better tests would allow access to ALL past information.
- Monthly results did not seem to work for the most part. Usually a price rise last month seemed to forecast a price rise this month. However, the low R2's indicate that we still haven't explained much of the price changes. So while RHW doesn't seem literally true, it is true that it is very difficult to accurately predict current prices from past prices.
- Annual data worked well for all 3 data series. Maybe the RWH works on the annual level, but not the monthly level... Perhaps to give a small incentive for traders to stay in business?
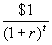 . This is how much money you would have to put in the bank today to have $1 t years from now.
. This is how much money you would have to put in the bank today to have $1 t years from now.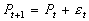 , where epsilon is an independently drawn random variable.
, where epsilon is an independently drawn random variable. 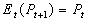 .
.