Prof. Bryan Caplan
bcaplan@gmu.edu
http://www3.gmu.edu/departments/economics/bcaplan
Economics 345
Fall, 1998
Problem Set #2 Answer Key
Wallace and Silver Problems.
2.4. Just minimize 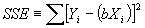 wrt b. This yields:
wrt b. This yields: 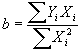
2.5.
a. If you add c to Y, a goes up by c; b stays the same. If you add c to X, a falls by bc; b stays the same. If you add c1 to X1, and c2 to X2, a falls by (b1*c1+b2*c2); b stays the same.
- Since you are subtracting a constant from each value of X, the intercept gets bigger: a goes up by
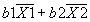 .
.
- a increases to a*c; b increases to b*c. If you multiply X by c, then the slope becomes b/c.
2.6.
- b=-1.63, a=79.941, R2=.8534.
- You need to use the equation you derived in 2.4, above, to get the slope for b: b=1.67. This means that the R2=-3.238. Impossible? What you have discovered here is that 0 £
R2 £
1 only if you include a constant term! If you don't have a constant, R2 doesn't mean anything.
- b=-1.63, a=0, R2=.8534. What you have learned here is that if you de-mean X and Y, then the constant becomes zero, but the R2 is unchanged. That makes sense, since the R2 is supposed to capture the percent of the variation we have explained. Demeaning variables does not change their variation.
- Since including a constant in a regression of y on x gives us a=0, leaving out the constant makes no difference. If you demean your variables AND omit the constant, the R2 is still meaningful.
Freedman and Lane Problems.
#1. Yes, you can find the regression line.  ;
; 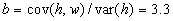 .
.
#3.
- Measurement error.
- b=.052; a=287.117
- 287.224; 287.276; 287.380; 292.580.
- Use the regression model because your expected measurement error is less!
- 287.117
- b=.052.
#5.
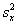 is just your estimate of the variance,
is just your estimate of the variance, 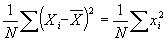 . So plug this in to yield
. So plug this in to yield 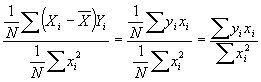 .
.
Caplan Problems.
- True. By definition,
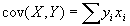 , and
, and 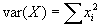 . So, cov(X,Y)/var(X,Y) is just the same as the formula for b derived in class.
. So, cov(X,Y)/var(X,Y) is just the same as the formula for b derived in class.
- By definition,
 . When b=0, a will just be
. When b=0, a will just be 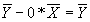 . Plugging in,
. Plugging in, 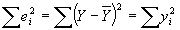 . QED. Since R2=1-SSE/TSS, R2=
. QED. Since R2=1-SSE/TSS, R2=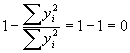
.
3.
- N=9
- k+1=2.
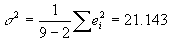
- The errors must sum to zero, but these sum to -1.
Computer Work.
See hw2ans.bin for the completed worksheet.
Interpretation of computing results: Nominal GDP and Real GDP are highly correlated (largely because they are both rising over time). Nominal GDP and M2 are high correlated (largely because money demand adjusted for income is stable - but don't worry about that now!). Unemployment and inflation have basically no relationship with each other, at least in the same year.
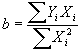
![]() wrt b. This yields:
wrt b. This yields: 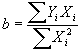
![]() ;
; ![]() .
.![]() is just your estimate of the variance,
is just your estimate of the variance, ![]() . So plug this in to yield
. So plug this in to yield 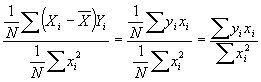 .
.