Prof. Bryan Caplan

bcaplan@gmu.edu

http://www.bcaplan.com

Econ 410

 

Week 2: The Logic of Collective Action

I.             Fallacies of Group Action

A.           People often think in terms of groups acting to promote their group goals.

1.            Workers/capitalists

2.            Oppressed minorities

3.            Women (and men?)

4.            Environment

5.            Northern business and the end of slavery

B.           Moreover, they often see groups pursuing their group-interest just as individuals pursue their self-interest.

C.           But there is a fundamental difficulty in this popular perspective: it amounts to a fallacy of composition.  Just because all members of group X would benefit if all members did something, it does not follow that it benefits any individual member to do so.

D.           Why?  Because frequently the benefits can be enjoyed just as well by people who did not pay the costs as those who did.  The benefits are social, but the costs are private.

E.           Ex:  Suppose one worker decides to just stay home and watch TV while the other workers foment revolution.

1.            Case 1: Revolution succeeds, all workers (supposedly) enjoy a brave new world - including the couch potato.

2.            Case 2: Revolution fails, all workers continue to suffer under the capitalist system - but at least the couch potato got to watch some amusing television programming.

F.            Key insight: marginal thinking.  If the same outcome will happen whatever you do, then selfishly speaking you might as well do personally benefits you, and quit worrying about the big picture. 

G.           Many people are appalled by this sort of thinking, but it is important to keep the positive and normative elements separate.  Maybe I do have a moral obligation to contribute, but that does not show that it advances my self-interest to contribute.

H.           We do need to be careful before we assert that there is no selfish reason to contribute.  As Olson emphasizes, frequently there are "byproducts" and other "selective incentives" that make contribution selfishly optimal.

1.            Ex: Trotsky on military discipline

II.            Individual Impact: Probability and Magnitude

A.           Saying that "The same thing will happen whatever you do" is admittedly overstatement. 

B.           It would be more precise to say "About the same thing will probably happen whatever you do." 

C.           In other words, you have to look at the probability you make a difference and magnitude of the difference you'll make, and compare then to your cost of acting.

D.           For example, it is possible that if you join the revolution, you will change the entire course of history.  Possible, but not likely!

1.            Still, there are several famous assassins who changed the course of history, and a lot of not-so-famous would-be assassins who came close.

E.           Similarly, if you give to starving children in Ethiopia, one more child could be saved.  That is a real difference, but it is a tiny magnitude relative to the size of the disaster.

F.            More relevant to public choice: the probability a vote matters and the magnitude of its impact.

G.           Voting increases the probability that your favored candidates wins, but how much does it increase that probability? 

H.           And even if your candidate does win as a result of your vote, how much will policy change?  As we will see next week, competing politicians typically wind up favoring quite similar positions.

III.          Calculating the Probability of Decisiveness, I: Mathematics

A.           When does a vote matter?  At least in most systems, it only matters if it "flips" the outcome of the election. 

B.           This can only happen if the winner wins by a single vote.  In that case, each voter is "decisive"; if one person decided differently, the outcome would change.

C.           In all other cases, the voter is not decisive; the outcome would not change if one person decided differently.

D.           It is obvious that the probability of casting the decisive vote in a large electorate is extremely small.  Recent events in no way refute this.  Losing by 100 or 1000 votes is a long way from losing by 1 vote!

1.            You might however say that Bush did win by a single vote on the Supreme Court!  But that is a voting body with only 9 voters.

E.           There is a technical formula for "guesstimating" the probability of decisiveness.  In spite of the difficulty, it is worth pursuing this issue in depth.  (If you haven't studied probability, just make sure you get the main idea).

F.            Suppose there are (2n+1) voters asked to vote for or against a policy.

1.            Note: Assuming an odd number of voters avoids the picky problem of ties.

G.           Then the probability that YOU are the decisive voter is the probability that exactly n voters out of the 2n voters other than yourself vote "for."

H.           Now suppose that everyone but yourself votes "for" with probability p - and "against" with probability (1-p).

I.             Then from probability theory:

J.            From this formula, we can see that the probability of a tie falls when the number of voters goes up.  Why? 

1.             gets smaller as n gets larger

2.             is less or equal to 1.  When you raise a number less than 1 to a larger power, it must get smaller.  (1 raised to any power is of course 1).

K.           Intuitively, the more people there are, the less likely one person makes a difference.

L.            This formula also says that as the probability of voter support goes above or below .5, the probability of a tie falls.  Why?

1.            When p=0, ; when p=1,  too.  In between p=0 and p=1, this term rises to a peak of  when p=.5, then falls.

M.          Intuitively, the more lop-sided opinion on a topic is, the less likely there is to be a tie.  If everyone agrees, a tie is impossible.

IV.          Calculating the Probability of Decisiveness, II: Examples

A.           What is neat about the above formula is that it allows us to say not just how the probability of decisiveness changes, but how much.  Let's work through some examples.

1.            Remember that the number of voters is (2n+1), not n.

B.           Example #1:  The close tenure vote.  n=10, p=.5. 

 

, or 17.8%.

 

C.           Example #2:  The easy tenure vote.  n=10, p=.8.

D.            

, or a little more than 1-in-500.

 

E.           Example #3:  The close county election.  n=5,000, p=.51.

 

, or a little more than 1-in-1000.

 

F.            Example #4:  The moderately close county election.  n=5000, p=.53.

, a little less than 1-in-8 billion.

G.           Example #5:  The close national election.  n=50,000,000, p=.501.

 

 

1.            For perspective: Imagine a lottery with a 1-in-100,000,000 chance of winning.  The probability of casting the decisive vote is less than the probability of winning that lottery 11 times in a row!

H.           Example #6:  The moderately close state election. 

n=2,000,000, p=.51.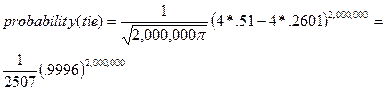 

a chance smaller than 1 in 10-100!  (My calculator just says 0).

I.             Upshot: For virtually any real-world election, the probability of casting the decisive vote is not just small; it is normally infinitesimal.  The extreme observation that "You will not affect the outcome of an election by voting" is true for all practical purposes.

J.            Even if you were to play around with the formula to increase your estimate a thousand-fold, your estimated answer would remain vanishingly small. 

1.            Ex: Adjusting for the Electoral College.

V.           Efficiency and Collective Action

A.           In collective action situations, the privately optimal level of participation is extremely low; but high participation is often the socially optimal outcome. 

B.           Why?  Frequently, everyone benefits a little bit if one more person participates.  The extra benefits for the participant are small.  But if you multiply them by millions of beneficiaries, the total benefits will often still exceed the total costs.

C.           The social efficiency of additional participation is not as clear for elections, as we will see; but when people urge you to vote, perhaps they are thinking that more participation is a public good.

D.           We can also think in terms of "public good for a group."  Higher Albanian turnout may not be a public good for everyone, but it might be a public good for Albanians.

VI.          Empirical Evidence on Collective Action Problems

A.           One way to get a feel for the logic of collective action is to see how little participation in politics there is.  Survey of adult Americans from Dye and Zeigler:

Activity

%

Run for public office

<1

Active in parties and campaigns

4-5

Make campaign contribution

10

Wear button or bumper sticker

15

Write or call a public official

17-20

Belong to organization

30-33

Talk politics to others

30-35

Vote

30-55

B.           Many experiments have been run to help improve our understanding of collective action problems. 

1.            Part of the design: Rule out "selective incentives" accounts of apparently unselfish behavior.

C.           Standard design: 

1.            I hand out a roll of 100 pennies to each person in the class. 

2.            Then, people are allowed to secretly put any number of their pennies into a jar. 

3.            You personally get to keep the pennies you don't put in the jar.

4.            I count the number of pennies in the jar; then I distribute twice that many pennies to the class, with each person getting the same share.

D.           What maximizes the total income of the class?  100% donation by everyone!

E.           What maximizes your private income?  0% donation!  No matter how little you donate, you still get an equal share.

1.            Caveat: This is only true if there are 3 or more players, yourself included.

F.            The first couple of times you do an experiment like this, you typically get moderate to high levels of donation - 50-80%.

G.           Donation levels usually begin falling as you repeat the experiment with the same group.  After a while, donation levels often fall to around 20%.

1.            For practical reasons, experiments usually only last a day or less.  So we can still speculate about what would happen if people played this game 10 times a day for a year.  I would expect donation levels to fall much more.

H.           Donation levels usually decline as the number of participants rises. 

I.             The less secrecy there is, the higher the level of donation.

J.            Conclusion: While the "logic of collective action" appears to exaggerate the degree of human selfishness, cooperation in these experiments is way below the group-income-maximizing level.

VII.        The Paradox of Public Good Provision

A.           People often appeal to the "logic of collective action" to justify corrective government policy.  Public goods problems don't "solve themselves."

B.           Problem: Isn't monitoring the government to act in socially beneficial ways itself a public good?

C.           Paradox: If citizens can voluntarily produce the public good of monitoring government, why can't they solve other public goods problems without government?  And if they can't voluntarily solve this problem, what reason is there to expect government to improve matters?