Bryan Caplan
bcaplan@gmu.edu
http://www3.gmu.edu/departments/economics/bcaplan
Econ 637
Spring, 1999
Weeks 8-9: Estimation and Identification of Systems of Simultaneous Equations
- Simultaneity and Simultaneity Bias
- So far it has been assumed that the behavior of the dependent variable can be described by a single equation. But even very simple of economic theories - like supply and demand - say that you need more than one equation to describe the behavior of the dependent variables.
- So what happens if you ignore this fact, and try to e.g. figure out the relationship between price and quantity by just regressing quantity on price?
- Question: Is this a supply curve or a demand curve that you've estimated?
- Let's try and see. The S&D model is defined by two equations:
- (S) Q+a
P=u1
- (D) Q+b
P=u2
- Solving for Q and P as functions of u1 and u2 yields:
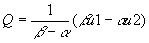
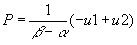
- Now what happens if Q is regressed on P? The estimated slope (excluding a constant) will be:
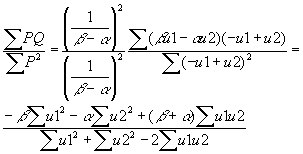
- Taking the plim of the slope yields:
 which is a biased and inconsistent estimator of BOTH the supply AND the demand equations! Instead you get a weird weighted average of the two coefficients.
which is a biased and inconsistent estimator of BOTH the supply AND the demand equations! Instead you get a weird weighted average of the two coefficients.
- Exceptions:
- As Var(u1) goes to infinity, the above estimator becomes a consistent estimator for -b
.
- As Var(u2) goes to infinity, the above estimator becomes a consistent estimator for -a
.
- If P and Q are part of a simultaneous system, regressing one on the other gives biased estimates for both supply and demand parameters. The resulting "mongrel" coefficient is simply meaningless except in polar cases.
- Exogeneity and Endogeneity
- Another term for simultaneity bias is "endogeneity."
- A variable is "endogenous" if it is "determined within the system." For example, P and Q.
- A variable is "exogenous" if it is "determined OUTSIDE the system." A common example in the S&D context is weather: weather can change P and Q, but P and Q don't change the weather. Econometrically, exogenous variables are independent of current and future disturbance terms.
- In general, a system of simultaneous equations that ONLY has endogenous variables will be impossible to estimate. (Exceptions to be discussed later).
- But if there are some exogenous variables (in particular, exogenous variables that matter only for SOME of the equations in the system), then it may be possible to estimate at least some of the equations in the system.
- Intuitively, why is this so? Suppose that we add weather to the earlier S&D system:
- (S) Q+a
P+g
W=u1
- (D) Q+b
P=u2
- Changes in weather shift the S curve. And the shifting of the S curve allows us to identify the D curve!
- Note: It is the exogenous variable in the (S) equation that lets us figure out the coefficients in the (D) equation. We still have no way to figure out the coefficients in (S).
- Now suppose that we add an exogenous income variable to the (D) equation, so that:
- (S) Q+a
P+g
W=u1
- (D) Q+b
P+h
I=u2
- Now the shifting of weather lets us trace out the (D) curve, and the shifting of income lets us trace out the (S) curve.
- Big problem #1: How do you ever really know if a variable is exogenous? Isn't it possible that weather changes quantity, but e.g. due to global warming, quantity changes weather? Surely if you run a randomized double-blind experiment you can know, but otherwise, it is quite difficult!
- Big problem #2: How do you ever really know if a variable only appears in one equation? Couldn't e.g. weather change not only the supply of oranges (more rain yields more abundant harvests), but also (maybe people want more citrus when there is hot, dry weather) the demand?
- Simultaneity and IV
- Probably the best way to handle simultaneity is to find a natural experiment instead of using historical data.
- Failing that, the simplest procedure econometric procedure is known as instrumental variables (IV); it also goes by the name of two-stage least square (2SLS).
- To perform IV, you need to find a matrix of instruments for X, Z. If X has k columns, then Z must have a minimum of k columns.
- Z must satisfy two properties:
- The variables in Z are correlated with those in X.
- Both income and weather will be correlated with price.
- The variables in Z are NOT correlated with the disturbance term u.
- If income and weather really are exogenous, then this holds.
- Where do the columns of Z come from?
- All of the exogenous variables in X.
- All of the exogenous variables in OTHER equations in the system.
- Note: If all exogenous variables appear in all equations, IV won't work! You need at least as many instruments as there are columns of X. Recall the intuitive interpretation of this.
- What does one do with Z? For each equation you are interested in:
- First, regress each column of X on ALL of the columns of Z to get a matrix of fitted values, X*. X*=Z(Z’Z)-1Z’X=PX. Note that if a variable X1 is in both X and Z, then regressing X on Z will yield a "fitted value" for X1 identical to the original value.
- Second, regress Y on X*, to get:
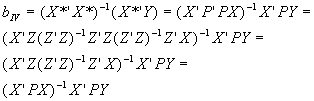
- It can be proven that bIV is consistent, and that var(bIV)=s
2(X’PX)-1.
- Example: the 3rd S&D model considered above:
- (S) Q=-a
P-g
W+u1
- (D) Q=-b
P-h
I+u2
- What are the instruments going to be? W and I.
- To estimate (S), regress P on W and I, yielding a fitted value for P. You also regress W on W and I, yielding unchanged fitted values equal to W.
- Then, regress Q on the fitted value of P and W.
- What could have been done with the 2nd model? What could not have been done? Explain econometrically and intuitively.
- Simultaneous Structural Equations, I: Vector Notation
- It is convenient to develop vector notation for systems of simltaneous equations. Consider an arbitrary system of G equations Byt+Cxt=ut, where B is a GxG matrix of coefficients of endogenous variables, C is a GxK matrix of exogenous variables, yt is Gx1, xt is Kx1, and ut is Gx1.
- Note: This means you have (G+K) variables and G equations.
- Note further that what is normally the left-hand-side variable is counted as one of the (G+K) variables.
- Example: Consider two equations (note the acceptability of arbitrary normalizations):
- (D) y1t+b
12y2t+g
11=u1t
- (S) b
21y1t+y2t+g
21=u2t
- In terms of vector notation, G=2, and K=1. These two equations could thus be written as: Byt+Cxt=ut, where the y's are endogenous variables (P and Q in this case) and the x's are exogenous variables (just the vector of 1's in this case), the u's are disturbance terms, and B (2x2) and C (2x1) are blocks of coefficients.
 ,
, 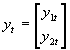 ,
, 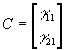 ,
, 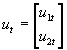
.
- Simultaneous Structural Equations, II: Reduced Forms and the Simulteneity Problem
- Notice that the reduced form of such a system of equations can be derived by subtracting Cxt from both sides and pre-multiplying by B-1 to get: yt=-B-1Cxt+B-1ut. For simplicity, you can define new variables so that you just have yt=P
xt+vt, where P
is GxK.
- Mathematically, then, what is the simultaneity problem? The problem is that estimating the reduced form gives you P
=B-1C, but what you want to know are the structural coefficients B and C!
- Economically, what is the problem? The problem is that the readily-estimated reduced forms are mere correlation, whereas the difficult-to-get structural coefficients are the causal sensitivities of interest.
- How do you get at the structural coefficients? As before, you need exogenous shifter variables that appear in one equation but not the other.
- But what are the general principles of identification, that will enable you to cope with more than merely a S&D system? And what is the basis for these general principles, both mathematically and intuitively?
- Simultaneous Structural Equations, III: General Principles of Identification
- The system Byt+Cxt=ut can be written even more compactly as
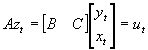
, where A is a Gx(G+K) matrix of all structural coefficients, and zt is the (G+K)x1 vector of all variables at time t.
- Note: by definition, BP
+C=0. Rewrite this as: AW=0, where A remains a Gx(G+K) matrix of all structural coefficients, and
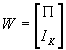
, which is (G+K)xK.
- Recall that it is quite possible for a system to be partially identified; e.g. D but not S is identified because you have a weather variable to shift S. What will be learned will be rules for determining if an individual equation in a system is identified.
- Individual equations are written as:
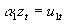 , where a
1 is a (G+K) row vector of all the coefficients in the first equation in the system.
, where a
1 is a (G+K) row vector of all the coefficients in the first equation in the system.
- Similarly, write the first row of AW=0 as
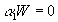 . Since a
1 is 1x(G+K), and W is (GxK)xK, this provides K equations restricting the behavior of the (G+K) equations of a
1.
. Since a
1 is 1x(G+K), and W is (GxK)xK, this provides K equations restricting the behavior of the (G+K) equations of a
1.
- Mathematically, then, the problem is that for a single unrestricted equation, you have (G+K) structural unknowns, but only K equations. To get identification, it is necessary to get some more equations.
- These additional equations come from a priori restrictions. The most common such restriction is that a variable equals zero, but other restrictions work too. Write these restrictions as
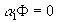 , where F
is (G+K)xR, R being the total number of a priori restrictions imposed on a
1. E.g.,
, where F
is (G+K)xR, R being the total number of a priori restrictions imposed on a
1. E.g., 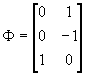 .
.
- Notice: the necessity of introducing substantive a priori restrictions to get econometric results is rarely talked about, but it has great methodological significance.
- Combining both sets of equations for a
1 yields:
 , which gives (K+R) equations for the (G+K) unknowns in a
1.
, which gives (K+R) equations for the (G+K) unknowns in a
1.
- It might appear that (G+K) equations are necessary to solve for all (G+K) unknowns. However, since the set of equations was not initially normalized, we actually only need (G+K-1).
- Therefore, in order to achieve identification, the number of equations (K+R) must equal or exceed (G+K-1) the number of unknowns minus 1. Subtracting K from both equations leaves us with a fundamental result: R³
(G-1). The number of a priori restrictions must equal or exceed the number of endogenous variables minus 1.
- Special cases:
- If R<G-1, then you are underidentified aka "unidentified." It is then impossible to back out structural coefficients from the reduced form.
- If R=G-1, then an equation is just identified aka "exactly identified."
- If R>G-1, then an equation is overidentified. There is nothing wrong with this, since your statistical fit is never perfect anyway.
- The condition that R³
(G-1) is known as the necessary order condition for identification. There is a subsidiary condition, known as the rank condition, that technically must also be satisfied, but you are not responsible for it.
- Simultaneous Structural Equations, IV: Estimating Identified Equations Using IV/2SLS
- One acceptable method of estimating structural coefficients of identified (i.e. just identified or overidentified) equations is to separately apply 2SLS (aka IV) to each identified equation of a system.
- To apply 2SLS, just let your set of instruments be ALL of the exogenous (aka "predetermined) variables in the system. Perhaps surprisingly, lags of an endogenous variable are in fact exogenous (at time t, whatever happened in the past is fixed!). The whole set of exogenous variables is thus:
- All lagged endogenous variables in the whole system.
- All current and lagged exogenous variables in the whole system.
- Example #1:
Go back to the simple S&D system, with
- (S) Q+a
P+g
W=u1
- (D) Q+b
P=u2
- Is the first equation identified according to our general principles? No, because R=0, but G=2, and 0<(2-1). So it can't be estimated.
- Is the second equation identified according to our general principles? Yes, because R=1 and G=2, so 1=(2-1). So it can be estimated using W as the sole instrumental variable.
- Example #2:
How about a simple S&D system that looks like this?
- (S) Q=u1
- (D) Q+b
P+g
I=u2
- Is the first equation identified? Yes, because R=2 and G=2, and 2>(2-1).
- Is the second equation identified? No, because R=0 and G=2.
- Example #3:
How about:
- (S) Q+a
P+g
W=u1
- (D) Q+b
P+h
I=u2
- Is the first equation identified? Yes, R=2 and G=2 again.
- Is the second equation identified? Yes, R=2 and G=2.
- The Basics of GLS
- OLS estimation builds on strict assumptions about the structure of the disturbance terms. When you violate these assumptions, OLS is generally inefficient, leading to incorrect calculation of SEs.
- General strategy:
- Figure out how to transform Y and X so that the transformed disturbance terms satisfy standard assumptions.
- Then perform OLS on transformed Y and X!
- This is known as Generalized Least Squares, or GLS.
- Consider a case where Y=Xb
+u, with u~N(0,s
2W
). This differs from earlier examples in one way only: we've replaced the identity matrix I with a new matrix W
.
- W
has to be the right kind of matrix (technically, positive definite). It is then possible to use the fact that the inverse of every positive definite matrix can be factored as: W
-1=P'P. (Software can usually do this factorization for you).
- The GLS approach to estimating Y=Xb
+u, with u~N(0,s
2W
) is then straightforward: pre-multiply Y=Xb
+u by P, yielding PY=PXb
+Pu.
- Note the variance of Pu: var(Pu)=E(Puu'P')= s
2PW
P'=s
2PP-1(P')-1P'=s
2I.
- Since the disturbance vector Pu satisfies the assumptions of OLS, we can simply perform OLS on the transformed equation - and all of the standard results of OLS will hold for the transformed equation.
- Seemingly Unrelated Regressions (SUR)
- Suppose you have a system of m equations with no simultaneity problem.
- Equation i of this system is just Yi=Xib
i+ui, where Yi is nx1, Xi is nxki, and ui is nx1. Notice: the variables can actually be different in each equation!
- Should the equations be estimated singly or jointly? Estimating them jointly is known as the Seemingly Unrelated Regressions (SUR) approach. To perform SUR, stack all m equations, so that you have e.g.:
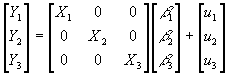 , where each row shown here is an entire equation.
, where each row shown here is an entire equation.
- For each individual equation, the X's and the u's are uncorrelated. But there could be correlation between the disturbances of different equations. Such correlation can be used to get more precise estimates. Thus, for the above equation,
 .
.
- Assume that E(uiuj')=s
ijI, where i,j=1...m.
- This means that within an equation (i=j), the homoscedasticity and nonautocorrelation assumptions hold.
- It further means that if i¹
j, there are contemporaneous cross-equation correlations, but no lagged cross-equation correlations.
- Thus,
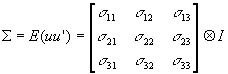
- With a variance-covariance matrix that looks like this, GLS rather than OLS is appropriate! But in order to perform GLS, it is necessary to estimate S
. The SUR technique is as follows:
- Apply OLS to each equation separately to estimate the sigma terms and construct an estimate of S
.
- Then, implement GLS on the whole mega-system of m equations: bGLS=(X'S
-1X)-1X'S
-1Y, and var(bGLS)=(X'S
-1X)-1.
- Two special cases: if s
ij=0 for i¹
j, or if X1=X2=...=Xm, then SUR reduces to OLS.
- Alternatives to 2SLS: 3SLS, MLE, GMM
- 2SLS throws out some valuable information by estimating each identified equation separately. Three more advanced techniques that estimates all of the identified equation in a system:
- Three-stage least squares (3SLS)
- Maximum likelihood estimation (MLE)
- Generalized Method of Moments (GMM)
- 3SLS
- 3SLS combines SUR and 2SLS.
- First estimate identified structural equations using 2SLS.
- Get residuals to estimate disturbance variance-covariance matrix.
- Apply GLS to entire system.
- MLE
- The central idea of MLE is that if the dependent variable Y is a function of an unknown parameter (or vector of parameters) q
, then your estimate of q
should be the value of q
that was most likely to have generated the observations Y. Thus, you want to maximize L(q
;Y).
- Doing MLE of the standard linear model yields conclusions similar to OLS, but not exactly the same. In particular, the (n-k) terms are generally replaced with just n - which we know to be biased. (The MLE's virtues are only asymptotic).
- More complicated MLE estimation of e.g. systems of equations must normally be performed by "numerical" methods rather than quickly applying some clean theorems to the data.
- Bad news: Complicated iterative search algorithms have to be used to figure out where the true maximum is; oftentimes it is hard to ever get an answer even from powerful computing software.
- GMM
- GMM is yet another alternative to LS that is becoming extremely popular as a method of estimating both single equations and large systems of equations.
- What GMM estimators involve:
- "Orthogonality conditions" - essentially just standard instrumental variable conditions that you assume are true at the population level.
- E.g. E(X'(Y-Xb
)=0
- You then look at the sample analog m(q
) using your actual data. Depending on what parameters you choose, you will be closer or further away from actually satisfying the conditions you assumed to hold at the population level.
- You want to minimize a weighted average of deviations from ALL of your orthogonality conditions. What weights? You want to find W, a heteroscedasticity and autocorrelation consistent estimator of [var[m(.)]]-1. (Don't worry about how; in practice the computer takes care of it).
- You then minimize the following wrt q
-hat:
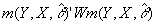
- In practice, GMM estimators must generally be calculated by "numerical" methods using canned software, but they don't have the same convergence problems that MLE tends to have.
- Advantages of GMM:
- Regardless of weighting matrix used, GMM is consistent and asymptotically unbiased.
- When optimal weighting matrix W is used, GMM is asymptotically efficient (in the class of estimators using orthogonality conditions).
- Errors don't need to be normally distributed or homoscedastic, provided they have zero mean.
- Implementing 2SLS, 3SLS, MLE, and GMM
- The Eviews method is the same for all four techniques. Type out your system of equations. After each equation, type an "@", then list your instruments.
- Then click on Estimate, and choose your preferred technique. Unfortunately, the student version doesn't have all of the options; but the computing difficulty (for you!) doesn't change when you move on to more advanced techniques.
- If any equation is underidentified, you get a singularity error.
- Comparing some estimated systems using 2SLS, 3SLS, ML, and GMM. All estimation is performed on the same set of international macro data.
- Model estimated:
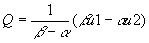
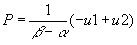
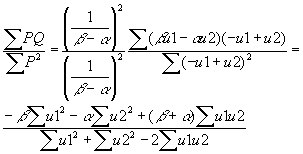
 which is a biased and inconsistent estimator of BOTH the supply AND the demand equations! Instead you get a weird weighted average of the two coefficients.
which is a biased and inconsistent estimator of BOTH the supply AND the demand equations! Instead you get a weird weighted average of the two coefficients.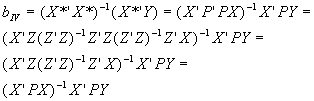
 ,
, 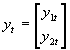 ,
, 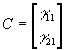 ,
, 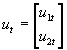
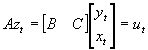
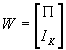
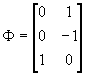 .
.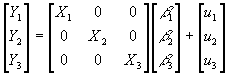 , where each row shown here is an entire equation.
, where each row shown here is an entire equation. .
.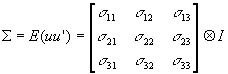
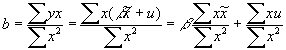 .
.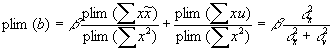 . The bigger the measurement error gets, the more biased towards 0 the estimator b becomes.
. The bigger the measurement error gets, the more biased towards 0 the estimator b becomes.