Bryan Caplan
bcaplan@gmu.edu
http://www3.gmu.edu/departments/economics/bcaplan
Econ 637
Spring, 1999
Week 10: Time Series, I: The Basics
- Univariate Time Series
- For most of this course, we have examined the statistical relationship between at minimum two variables. But an individual time series often contains interesting statistical relationships with itself - i.e., between current and past values.
- Not coincidentally, numerous economic theories imply relationships between the current value of a single variable and its lags.
- Random walk theories: financial markets, consumption, tax rates...
- Growth theory
- Q theory of investment
- Notation: the lag operator L(xt)=xt-1; Ls(xt)=xt-s; (1-L)xt=xt-xt-1.
- Note: The lag operator can often be algebraically manipulated as a scalar.
- Ex: Let A(L)=1-aL. (1-aL)* (1+aL+a2L2+...apLp)=1 as p goes to infinity. So A-1(L)= (1+aL+a2L2+...).
- Basic Autoregressive and Moving Average Processes
- There are two particularly common sorts of univariate times series: autoregressive (AR) processes, and moving average (MA) processes.
- The AR(1) process: ut=r
ut-1+e
t, with e
t~N(0,s
2).
- var(u) looks like:
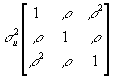
- Normally -1<r
<1.
- The unconditional expectation is E(ut)=0, although the conditional expectation Et(ut)=r
ut-1.
- var(ut)=s
u2=s
e
2/(1-r
2)
- Note: current disturbance ut is a weighted sum of the current shock and ALL previous shocks. It therefore has an infinite "memory."
- The MA(1) process: ut=e
t+q
e
t-1 with e
t~N(0,s
2).
- var(u) looks like:

- The unconditional expectation is E(ut)=0, although the conditional expectation Et(ut)=q
e
t-1.
- var(ut)=s
u2=s
e
2(1+q
2)
- Note: current disturbance ut is a weighted sum of the current shock and last period's shock. It therefore has a finite "memory."
- Stationarity of AR and MA Processes
- A process is stationary if its mean, variance, and covariances are independent of time.
- Consider the AR(1) process: yt=m+ayt-1+e
t.
- Note that you can use lag-operator notation to rewrite this as: (1-aL)yt=m+e
t. Then multiply both sides by (1-aL)-1 to get: yt=(1+aL+a2L2+...)(m+e
t).
- Finally, note that the lag of a constant is just the constant, so: yt=(1+a+a2+...)m+(1+aL+a2L2+...)e
t= yt=(1+a+a2+...)m+e
t+ae
t-1+a2e
t-2+...
- Is the above expression (an infinite summation) finite? It is so long as abs(a)<1. Then E(yt)=m/(1-a).
- What if a=1? Then summation is infinite, and there is no mean for the process (though of course an empirical mean will always exist).
- The AR(1) process is stationary so long as abs(a)<1. (See the text for deviations of var(yt) and r(yt,yt-s)).
- The AR(2) process: yt=a1yt-1+a2yt-2+e
t. Write this in lag notation: A(L)yt=e
t, with A(L)=1-a1L-a2L2.
- Something quite interesting can be learned by factoring A(L)=1-a1L=a2L2 as (1-l
1L)(1-l
2L), and using the quadratic formula:
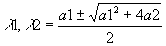 .
.
- Then:
- A-1(L)=1/[(1-l
1L)(1-l
2L)], so process has a finite mean so long as the absolute value of both roots is less than 1. (Alternately, a process has a finite mean so long as the modulus of each roots lies between 0 and 1.
- With complex roots, the process actually follows a sine wave (!); if the modulus of each root lies between 0 and 1, then the process follows a damped sine wave; otherwise an explosive sine wave. (!)
- In general, then, the AR(p) processes will be stationary so long as the modulus of each root - real or complex - lies between 0 and 1. Aka: "roots lie within the unit circle."
- Just as the dependent variable can follow an AR process, it can follow an MA process. E.g. MA(1): yt=e
t-be
t-1.
- Two interesting equivalencies:
- Recall that the AR(1) process (with zero mean) can be written as: yt=e
t+ae
t-1+a2e
t-2+... What is this? It is an MA(¥
)!
- The MA(1) process yt=e
t-be
t-1 can be inverted to get e
t=yt+byt-1+b2yt-2+..., which can be rewritten as yt=-byt-1-b2yt-2-...+e
t. What is this? It is an AR(¥
)!
- MA is always stationary; but the above inversion can only be performed if abs(b)<1. So for MA this is called the "invertibility condition" instead of the "stationarity condition."
- The general ARMA process combines the elements of both AR and MA processes. General form: A(L)xt=B(L)e
t.
- Stationarity in General
- To repeat: A series is stationary when the mean, variance, AND covariances are independent of time.
- Many econometric results implicitly assume stationarity.
So the general strategy for coping with non-stationarity will be the same one we have pursued many times before: Find a transformation that makes the series stationary, then proceed as normal.
- There are two quite different kinds of nonstationarity: explosive and non-explosive. An explosive process when shocked responds at a continually increasing rate; a non-explosive process does not.
- A random walk (aka "unit root"; aka "integrated") is a special kind of nonstationary, non-explosive process in which shocks are permanent.
- How can one tell that a random walk is not stationary? Consider Yt=a+Yt-1+ut. Its conditional expectation E(Yt|Y0)=at+Y0 is time-dependent. Similarly, var(Yt|Y0)=ts
2 is also time-dependent.
- Here is a table applying these concepts to five different processes:
|
Process Name |
Nonstationary? |
Explosive? |
Example |
Solution |
|
Stationary |
No |
No |
Yt=1+.95Yt-1+ut |
none needed |
|
Trend stationary |
Yes |
No |
Yt=1+.9Yt-1+5t+ut |
first difference as:
D
Yt=50+D
ut |
|
Random walk with drift |
Yes |
No |
Yt=a+Yt-1+ut. |
first difference as:
D
Yt=a+ut. |
|
Explosive |
Yes |
Yes |
Yt=1+1.05Yt-1+ut |
Hard: Differencing won't work |
|
Random walk with drift and trend |
Yes |
No |
Yt=1+Yt-1+5t+ut |
Difference twice to get: D
Yt-D
Yt-1=5+D
ut |
- Testing for Stationarity
- How do you know if your series is stationary or not? This is a quite complicated question that can only be touched upon here.
- Main problem: if you want to test the null of a random walk, then (because you have implicitly violated assumptions of OLS) coefficient/SE does not have standard t distribution.
- Alternate test statistics, beginning with Dickey-Fuller, developed to handle random walk null. If interested, see text.
- Main problem: low power. Often null of random walk can't be rejected, but null of stationarity can't be rejected either.
- Difficult problem, but not irrelevant to economics.
- Random walk theories of financial markets, consumption, and more.
- Are shocks to e.g. output permanent or transitory?
Appendix: GLS, Heteroscedasticity, and Autocorrelation
- Return to GLS
- OLS estimation builds on two assumptions that will now be considered in some detail:
- No heteroscedasticity of disturbance terms.
- No autocorrelation of disturbance terms.
- It can be proven that performing OLS on data that violate these two assumptions still yields unbiased and consistent estimates of the coefficient vector. However, OLS is inefficient, and leads to incorrect calculation of SEs.
- General strategy:
- Figure out tests for the presence of heteroscedasticity and autocorrelation.
- Then, GLS: Figure out how to transform Y and X in such a way that heteroscedasticity and/or autocorrelation disappears, then perform OLS on transformed Y and X.
- Heteroscedasticity and Its Detection
- The variance of a standard, homoscedastic disturbance vector looks like: var(u)=E(uu')=
 .
.
- The variance of a heteroscedastic disturbance vector, in contrast, looks like: var(u)= E(uu')=
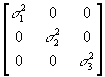 .
.
- Examples:
- Variance of commodity future prices throughout the year.
- Variance of expenditure on food may be greater for rich people than poor people.
- Many tests for heteroscedasticity; the most common one is the White test.
- First problem: disturbance terms unobserved. This is handled by using the observed error terms e=Y-Xb.
- Then, do OLS regression of e2 on all of your X variables, their squares, and their cross-products. (Eliminate redundant variables; call the number of nonredundant variables k').
- Under the null of homoscedasticity, n*R2 of this regression has chi-squared(k'-1) distribution.
- Correcting for Heteroscedasticity
- The most general correction: when you've detected heteroscedasticity, but don't know anything specific about its form, you use OLS coefficients, but "heteroscedasticity-consistent" SEs (HCSEs).
- To derive the HCSEs:
- Get the OLS error terms e=Y-Xb.
- Recall that the general formula for var(b) is E[(b-b
)(b-b
)']=E[(X'X)-1X'uu'X(X'X)-1]= (X'X)-1X's
2W
X(X'X)-1. (With homoscedasticity, W
is just the identity matrix, so it disappears and leave you with s
2(X'X)-1).
- Estimate s
2W
using the error terms as follows:
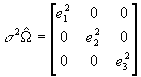 .
.
- Last, plug this into (X'X)-1X's
2W
X(X'X)-1. The square roots of the diagonals give you the HCSEs.
- More specific corrections require insight into the exact form of the heteroscedasticity. For example, if the variance of the disturbance terms depends entirely on income. Then
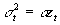 , and
, and 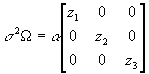 .
.
- This looks like a job for GLS. If
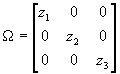 , then
, then 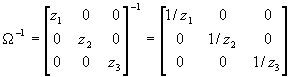 . Moreover, since P'P=W
-1, P=
. Moreover, since P'P=W
-1, P= .
.
- Following the rules of GLS, pre-multiply Y=Xb
+u by P, and do OLS on PY=PXb
+Pu. All of the assumptions of OLS now hold for this transformed relation, yielding
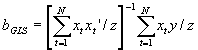
.
- Detecting and Correcting for Autocorrelated Errors
- In general, errors are autocorrelated when - for time series (regular or pooled), the off-diagonals of the disturbances' variance-covariance matrix are nonzero. For example, the error terms may follow an AR(1) or MA(1) process.
- The most common test for autocorrelation is the Durbin-Watson test. Use the e's from OLS to calculate
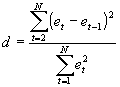 .
.
- Intuition: by construction E(e)=0, so errors are scattered around the x-axis. If e's are positively correlated, then the numerator term tends to be small; if the e's are negatively correlated, then the numerator tends to be large.
- Further intuition:
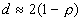 , where r
is the correlation between et and et-1. So if D-W is around 2, there is probably no autocorrelation; if it is less than 2, there may be positive autocorrelation; if it is greater, there may be negative autocorrelation.
, where r
is the correlation between et and et-1. So if D-W is around 2, there is probably no autocorrelation; if it is less than 2, there may be positive autocorrelation; if it is greater, there may be negative autocorrelation.
- Once you've calculated your D-W statistic, refer to the appropriate part of the table. You need to know both N and (k-1).
- A special feature of the D-W tables is that they provide lower and upper bounds; Johnston/DiNardo recommend treating the upper bound as the critical value.
- The test gives the values for positive autocorrelation; take 4-d to test for negative autocorrelation.
- Test only valid if you have a constant term in your original regression.
- You need a different test if the set of independent variables includes lagged dependent variables.
- Correcting for autocorrelation: while there are formal procedures for handling autocorrelation (often derived from the principle of GLS, discussed below), the easiest thing is usually to re-specify your regression.
- E.g., if you estimate yt=b
1+b
2Xt and find autocorrelation, try adding one or more lags of x or y. The autocorrelation will usually go away.

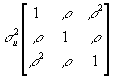

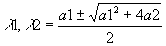 .
.  .
. 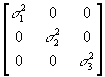 .
.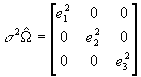 .
.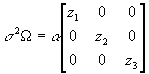 .
.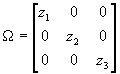 , then
, then 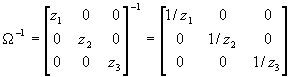 . Moreover, since P'P=W
-1, P=
. Moreover, since P'P=W
-1, P= .
.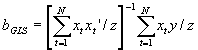
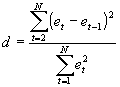 .
.