Bryan Caplan
bcaplan@gmu.edu
http://www3.gmu.edu/departments/economics/bcaplan
Econ 637
Spring, 1999
Week 12: Discrete and Limited Dependent Variable Models
- Discrete Choices
- Independent
dummy variables appear frequently in empirical work in economics, and pose no special econometric problems.
- Dependent
dummy variables appear less often, but are still common - and they do pose some special econometric problems.
- There is a large set of different kinds of variables that pose similar problems when they are dependent:
- Regular dummy variables
- Dummy variables that are derived from continuous variables - called "latent" or "index" variables.
- Unordered polychotomous variables (e.g. y=1 if you walk, 2 if you drive, 3 if you take the train)
- Ordered polychotomous variables (e.g. y=1 if you are in the top third of your class, 2 if you are in the middle third, and 3 if you are in the bottom third).
- Sequential polychotomous variables (e.g. y=1 if you finished high school, 2 if you had some college, 3 if you finished college, 4 if you hold an advanced degree).
- "Count data" - if the variable must take on an integer value.
- The Linear Probability Model
- The simplest way to deal with the problem of discrete dependent variables is to ignore the problem. Just treat it like any other left-hand-side variable and perform OLS.
- Natural interpretation: prediction of Y|X is the conditional probability of Y given X.
- Problem #1: Predictions are not constrained to lie between 0 and 1! This can make the interpretation of the results quite puzzling.
- Problem #2: Linear probability model is heteroscedastic. The residual ei equals either 1-Xib or -Xib since y equals either 0 or 1. Implied variance of disturbance term is condition on X: var(e
i|Xi)=Xib
(1-Xib
).
- Heteroscedasticity can be corrected with White procedure, but the problem of out-of-sensible-range predictions is harder to solve.
- Example of linear probability model.
- The Probit Model
- How can you constrain your predictions to lie between 0 and 1? Why not take some function of your result that maps the whole domain of real numbers into the 0-1 range? I.e., find a suitable F such that P(Yi=1)=F(Xib
).
- First attempt at this: the probit model. Let F be the cumulative density function of the standard normal distribution, traditionally denoted by F
(.)=
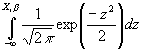 . Notice that the range of this F lies between 0 and 1.
. Notice that the range of this F lies between 0 and 1.
- Some rationale: Suppose your dependent dummy variable is derived from an unobserved continuous "latent" variable y*, such that yi=1 if yi*>0, 0 otherwise, where yi*=Xib
+e
i. (e
i~N(0,s
2), so y*|X is normally distributed).
- Then note that P(yi=1)=P(yi*>0)=P(Xib
+e
i>0)=P(e
i>-Xib
) =P(e
i/s
>-Xib
/s
).
- Since y* is normally distributed, this is equal to P(e
i/s
<Xib
/s
)= F
(Xib
/s
), the probit distribution.
- Simply doing a linear regression and plugging it into the standard normal cdf to find out the parameters for the probit would make no sense.
- Rather, we want to estimate F
(Xib
) using MLE. This technique makes sense, since it will tell us what value of b
is most likely to have generated our observations given that P(Y|X)=F
(Xib
).
- There is no clean solution to the probit; rather, the MLE is discovered numerically by your canned software. As explained earlier, the computer begins with some initial values and performs search algorithms (like checking the derivatives and moving in the suggested direction) until further iterations yield no significant improvement.
- Nice feature of the probit is that since the likelihood function is globally concave, the local max is also the global max.
- Example of probit.
- The Logit Model
- The logit is extremely similar to the probit, and attempts approximately the same mission. The only difference is that the logit has a different F.
- Instead of F=F
(Xib
), the logit uses F=L
(Xib
), where lambda is the logistic distribution:
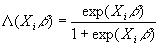 . Notice that this must lie between 0 and 1.
. Notice that this must lie between 0 and 1.
- The logit, like the probit, is calculated numerically using a MLE routine.
- Like the probit, the local max of a logit is also the global max.
- Example of a logit.
- Linear Probability, Probit, and Logit Compared
- In the attached example, all three models were applied to estimate the conditional probability of being at war. In the linear probability case, the War dummy was simply regressed on a constant, real output growth, lagged real output growth, inflation, and lagged inflation.
- For the probit and logit estimation, the regression model was simply inserted into the brackets of the probit and the logit; then Eviews estimated the coefficients using MLE.
- The tstats look similar, but nothing else does on the initial page of output.
- But doing simulations shows that the predictions are virtually identical. The three pages show the three models predictions of the probability of war, conditional on the growth rate of real output -3 to +7%), for three different rates of inflation (0%, 10%, 150%).
- W1 is linear probability.
- W2 is logit.
- W3 is probit.
- The Ordered Probit
- Suppose that you have defined three discrete variables by partitionining an unobserved continuous variable.
- E.g.: y1=1 if you don't work at all; y2=1 if you work part-time; y3=1 if you work full-time (and 0 otherwise in all three cases). These three discrete variables are a function of the continuous variable, y*=hours worked: y1=1 if y*<c1; y2=1 if c1£
y*<c2; y3=1 if y*>c2.
- You could then estimate the ordered probits (or logits) using MLE:
- P(y1=1)=F(c1-Xb
)
- P(y2=1)=1-F(c2-Xb
)-F(c1-Xb
)
- P(y3=1)=1-P(y1=1)-P(y2=1)=1-F(c2-Xb
)
- Your output estimates not only the b
but the c's.
- What are the c's? The c's are estimates of the "limit points" that sub-divide the sample. (You lose one of the c's - let it be c1 - in estimation, but you still get estimates of relative spacing of categories).
- In general, if you are doing probit-type estimation but realize that you can sub-divide your estimates into 3 or more categories - and think that might be interesting - ordered probit (or ordered logit) is the way to go.
- The Tobit
- Data can be either truncated or censored.
- Data is "truncated" when both the X's and the Y's are missing.
- Data is "censored" if we have the X's but not the Y's.
- Censoring issues sometimes arise with discrete estimation. Why? Because when the dummy is 1, we may actually see what happens, and when the dummy is 0, we don't.
- Ex: Predicting the taste for cars. If you buy a car, we can also observe how much you pay; but if you don't buy, we don't know anything specific about your taste for cars.
- Contrast with the classic truncation problem of the Roman soldier.
- One way to cope with censored dummy data is to use the Tobit (aka "Tobin's probit"), which is a simple extension of the probit. A Tobit applies MLE to estimate: yi=max{0, Xib
+e
i). See text for specifics.
- Estimating regular model on censored data leads to attenuation bias.
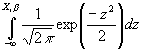 . Notice that the range of this F lies between 0 and 1.
. Notice that the range of this F lies between 0 and 1.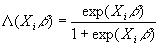 . Notice that this must lie between 0 and 1.
. Notice that this must lie between 0 and 1.