Prof. Bryan Caplan

bcaplan@gmu.edu

http://www.bcaplan.com

Econ 812

Week 2: General Equilibrium

I. Strategic Interaction Between Maximizers

A. Economists usually think of individual agents as maximizing something, but rarely analyze individuals in isolation. For social scientists, interesting questions almost always involve more than one individual.

B. Such interesting questions are however analytically challenging. When one person "plays against nature," the action is one-sided. You do not need to worry about how your "opponent" will change its behavior in response to your behavior. Once there is more than one person, you do.

1. Even this is oversimplified, since animals can play strategically to some degree. But no one e.g. expects wolves and rabbits to form an alliance against hunters.

C. Given the complexity of the problem, economists have focused a lot of time on a very easy case. Imagine that there are not just more than one agent, but a lot of agents. So many, in fact, that you do not have to worry about how other actors will strategically respond to your decisions.

1. There are many examples of this kind of thinking. When you buy corn, you do not contemplate how corn farmers will respond to your purchase.

D. Interesting result: Once you make the problem easy in this one way, you can make it extremely complex in other ways, and still get clear answers. Analysis of complex economies from this starting point is known as general equilibrium theory.

II. Examples of General Equilibrium

A. Simple example: Suppose I consumers have identical preferences and endowments in a two-good economy. U=a ln x + b ln y; a+b=1. These agents make exchanges in markets where they know their personal behavior has no perceptible effect on prices.

B. What happens? Intuitively, this situation is sustainable only if prices induce everyone to consume their own endowment!

C. Formally: We can substitute out for y by noting that , and in a commodity economy, , so agents maximize: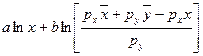

D. Differentiating, we learn that: . Since agents consume all of their income: , , the usual constant-income-fractions result.

E. Now simply find the prices that induce everyone to consume their initial endowments. Set , . Then you have 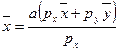. Simplifying, we learn that: . The equilibrium price of x is directly proportional to the taste parameter for x and the initial endowment of y; the price of y is directly proportion to the taste parameter for y and the initial endowment of x.

F. What if we make things more interesting by allowing for taste and endowment differences? Specifically, each agent i has U_i=a_i ln x + b_i ln y, and endowments and . Then what?

G. Now agents are actually going to make trades at equilibrium prices, instead of just noting that prices leave no incentive to trade. So we have to find the prices that induce aggregate consumption to equal aggregate endowments, taking the full interaction between prices and consumption into account.

H. Formally, add up I equations for individual consumption of x as a function of prices and initial endowments. Then impose the constraint that . This gives us: . Solving, we find that: 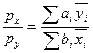. Once again, we have solved for prices as a function of preferences and initial endowments.

1. Note: We would get the same result if we solved for y instead. Intuitively, if there are two markets and one clears, so does the other.

I. Worth noticing: Utility function implies that people will give up anything to have a finite quantity of each good. If half of the people had no x, and the rest had both, why couldn't the no-x-ers be induced to give up practically all of their y?

III. General Equilibrium in Pure Exchange Economies

A. General equilibrium problems can be analyzed in very general terms.

B. Formally, assume:

1. There are I consumers indexed i=1,...,I.

2. There are K commodities indexed k=1,...,K.

3. Commodity consumption must be non-negative.

4. Utility U_i(x) is strictly increasing in all commodities (stronger than necessary, but simpler).

5. Consumers start with endowments of commodities; endowment of consumer i is eⁱ.

6. There is a continuous market price vector p=(p₁,...,p_k) that agents treat as exogenous.

C. Then let us define general equilibrium to be a situation in which:

1. Consumer i maximizes U_i s.t. px£peⁱ for all i.

2. Aggregate consumption never exceeds aggregate endowments: .

D. Intuition: Since endowments and utility functions are fixed, what varies to make an equilibrium possible? The consumption vectors, x. And what changes consumption vectors? Naturally, the price vector, p.

IV. Sufficient Conditions for Existence of General Equilibrium

A. Caveat: General equilibrium might still exist even though sufficient conditions not met!

B. First, note that the inequalities can be replaced with equalities because utility functions are strictly increasing.

C. Second, note that since this is an endowment economy, multiplying all prices through by a scalar l changes nothing; if p is an equilibrium price vector, so is lp. So we can restrict attention to price equilibria where .

D. Then the following assumptions guarantee the existence of general equilibrium.

E. Assumption 1: U_i(p) has a unique solution for all i and all p.

F. Assumption 2: Total demand for good k exceeds total endowment for a small enough p_k, and falls short of total endowment for a large enough p_k.

G. Assumption 3: The total demand function for k is continuous in p_k for 0<p_k<1.

H. In a 2-commodity world (k=2), you can prove the existence of general equilibrium using the Intermediate Value Theorem. If one market clears, the other has to clear, and if demand is continuous and can be too high or too low, it must at some point be just right.

I. In a k-commodity world, you can prove the existence of general equilibrium using Brouwer's Fixed Point Theorem. Basic idea of fixed point theorems: find conditions for functions such that there must be an f(x)=x. All of our assumptions together conveniently satisfy Brouwer's Fixed Point Theorem, so QED.

J. How do you get to these fixed points? GE theory usually focuses on the "Walrasian auctioneer" who adjusts price vectors to eliminate excess demands. (Austrians tend to hate this). We will discuss alternatives later.

V. Counter-Examples

A. When would a general equilibrium not exist? Each of the assumptions is made for a reason. Some of the more notable possible reasons for non-existence:

B. Counter-example #1: Lexiocographic preferences, hence no utility function. No prices would induce people to give up the lexicographically preferred commodity.

C. Counter-example #2: Discontinuity. If total demand for x is 90% of endowment at p=.7, and 110% of endowment at p=.7-e.

D. Counter-example #3: Demand not "well-behaved" at extreme prices. This might simply imply 0 prices for some goods, but there may be technical complications.

E. Counter-example #4: Prices are discontinuous. If prices have to be in discrete 1-penny units, for example, general equilibrium may not exist.

F. Remember: Standard theorems give sufficient conditions. G.E. might exist anyway. Ex: Linear utility functions, where U=x+y. What assumption does this violate? Can you describe the G.E. anyway? (Hint: What happens to demand for x if the price of x exceeds the price of y? Vice versa?)

VI. The Two Welfare Theorems

A. Market-clearing prices in individual markets have familiar welfare properties. At the intersection of S&D, total surplus is maximized, so the allocation must be Pareto efficient.

B. But can these results be generalized to multiple markets? General equilibrium theory can prove that the results from simple S&D cases generalize broadly.

C. First Welfare Theorem: Under the previous assumptions, the general equilibrium allocation is Pareto efficient.

D. There is a standard proof by contradiction. Suppose that x is an equilibrium allocation but x' is Pareto superior to x.

1. Then since x' must be feasible, .

2. Then since prices are non-negative, .

3. Since utility is strictly increasing in consumption, .

4. This implies that .

5. BUT: By the definition of Pareto improvement, all consumers must weakly prefer x' to x, one must strictly prefer x' to x. Weak preference requires that x' not be more affordable than x: . Strict preference requires that x' be not affordable for some i, so for at least one person, .

6. Summing up these weak and strong inequalities implies that: , contradicting (4).

E. Many economists find this welfare theorem less than compelling. After all, an allocation where one person owned everything is also Pareto efficient. But these economists often find hope in the second main result (some additional assumptions on utility functions are needed, and I omit the proof):

F. Second Welfare Theorem: Any Pareto efficient allocation can be a general equilibrium given some initial endowments.

G. Standard interpretation: Just by changing initial endowments ("redistributing") in the right way, you can make any Pareto efficient allocation self-sustaining.

H. Philosophical perspective: All distributive complaints against competitive markets can be answered with some form of lump-sum redistribution. Mere existence of the market does not make any efficient equilibrium unsustainable.

I. Possible contrast: Democracy.

VII. Arrow-Debreu Contingent Claims Markets

A. General equilibrium already seems rather general. But Arrow and Debreu noticed that it was much more general than anyone realized.

B. G.E. can handle intertemporal markets. Just think of good k at time t as a different good than k at time t+1. Instead of trading current goods, you can trade promises to deliver goods at any time.

C. Ex: I have an endowment of bananas in 2016 that I can trade just as if there were physical bananas in my hands.

D. More impressively, G.E. can handle an arbitrary level of uncertainty. Just think of good k if x happens to be a different good than k if not-x happens.

E. Ex: I have an endowment of bananas in 2016 if average temperature exceeded 80 degrees. I can trade this contingent claim just like I had some physical bananas right now.

1. Imagine taking an unconditional claim and ripping it into pieces, each of which specifies the conditions under which it pays off.

F. In both cases, the problem is isomorphic to the standard one, so all of the standard results go through.

G. Natural extension: Betting markets.

H. Particularly interesting: You can analyze contingent claims markets without specifically talking about time preference or probabilities.

VIII. Application: Intertemporal Consumption

A. Macroeconomists often analyze consumption over time. How can you move from individual (or small country) analysis to general equilibrium?

B. Once again, the trick is to find the prices that induce aggregate consumption to equal aggregate endowments. In intertemporal markets, such prices are usual known as interest rates.

C. So suppose the world is populated by identical infinitely-lived agents who maximize , and have a given endowment stream.

D. Standard result is that each individual sets . If , you consume less every period; if , you consume more every period.

E. But what happens in general equilibrium? In general equilibrium, consumption must equal endowments in every period. Therefore, if endowments are constant and people have identical preferences, .

F. Similarly, if endowments are growing at a rate (1+g), people want to smooth consumption by borrowing against their future income. So interest rates in general equilibrium must rise high enough that people are content consuming their current endowment and no more. This happens when . Expected growth raises interest rates today!