Prof. Bryan Caplan

bcaplan@gmu.edu

http://www.bcaplan.com

Econ 812

Week 5: Repeated Games, Competition, and Cooperation, I

I. Finitely-Repeated Games

A. We frequently play with the same people over and over again.

B. Question: If players condition their behavior in one game on your behavior in previous games, what happens?

C. Answer: More equilibria may be sustainable.

D. There are two main cases to consider: finitely-repeated games and infinitely-repeated games.

1. Note: Games that probabilistically end, with no fixed upper bound to number of games, count as infinitely-repeated.

E. Suppose two players first play a PD game, then a Coordination game, using last week's payoffs.

F. Note: The "independent" equilibria of the two games remain equilibria.

G. But a Pareto-superior outcome now becomes possible. Suppose that each player plays Left in the second game if either player failed to Cooperate in the first game, and Right otherwise. Then both players play Cooperate, Right, and this is a NE!

H. How is this possible? If a player fails to Cooperate in the first game, he gets 6, but then only earns 3 in the second game, for a total payoff of 9. But equilibrium play has a payoff of 10.

I. What happens if you reverse the order of the two games?

II. The Paradox of Backwards Induction

A. Thus, even in finitely-repeated games, the set of Nash equilibria expands. But it expands much less than you would think.

B. How so? Suppose two players play the PD game a hundred times. Couldn't they sustain Cooperation by threatening retaliation?

C. No. In the last turn, both players will defect. Since they both defect in the last turn no matter what, threatening to defect if your opponent fails to cooperate in the second-to-last game is no deterrent at all. So people fail to cooperate then, too,

D. Pushing this logic backwards all of the way to the first turn, cooperative play completely "unravels."

E. How does this differ from the previous example? That combined a dominance-solvable game with a game with two Nash equilibria. So even in the last turn, a sort of "revenge" is possible. Not so if all of the games in the series are dominance solvable.

F. Aside: In reality, of course, experiments confirm that people do cooperate in finitely-repeated games to a greater extent than 1-shot games. Some attempts have been made to theoretically model this. Most are based on the premise that players assign a small probability of irrationality to their opponent.

III. Infinitely-Repeated Games

A. Few games literally last forever, but many games always have a chance to continue. As long as they have that chance, game theorists call them "infinitely repeated."

B. With infinite repetition, the previous unraveling logic no longer holds, making more equilibria sustainable. Now, the intuition of retaliation works.

C. Simple example: Repeated PDs. Suppose we both make the most extreme possible threat (aka "trigger strategy"): If you cheat me once, I'll never cooperate with you again. Suppose further that we both discount the future by b. (Alternately, that the game continues each turn with probability b). Is this a NE?

D. If you cooperate, you get . Recalling the formulae for infinite sums, this adds up to .

E. If you defect, you get 6 immediately, but then only 1 forever afterwards. Mathematically: , which adds up to: .

F. To check to see whether this is a NE, then, we see whether the Nash payoff weakly exceeds the defection payoff. Is ? It is, so long as b³1/5.

1. Note: Without discounting, repeated games are a no-brainer. No finite gain from cheating would ever be worth infinite punishment.

G. Are other equilibria sustainable? Of course. You might not cooperate at all. You might only punish for one period, then return to cooperation. Intuition: The weaker the punishment, the higher b must be to make cooperation sustainable (b³1/4 in the latter case).

H. The Folk Theorem shows that if cooperation is sustainable at all, there will normally be an infinite number of equilibria.

I. So what actually happens out of the endless possibilities? As in Coordination games, focal points probably matter a great deal, but are hard to formally model.

IV. Reputation

A. Economists frequently invoke reputation to explain seemingly money-losing behavior. Does this make sense?

B. Yes. The logic of repeated play often works even if there is some one-shot interaction. Suppose, for example, that a store owner decides to cheat or not cheat a customer, and one-time customers decide whether to buy or not.

	Buy	Don't
Cheat	10,-2	0,0
Don't	5,2	0,0

C. Using weak dominance, the store owner always cheats, so the customer never buys.

D. But suppose that customers know whether the store has cheated in the past, so they can play (Buy if no past Cheating, Don't otherwise).

E. Is this a NE? It is if .

F. The applications of reputational models are endless. Most obviously, reputation is the market alternative to regulation of product quality and the like.

1. Question: How does ease of detection affect reputational incentives?

G. Reputation probably matters for prices as well as quality. Stores may keep prices below daily profit-maximizing levels because they want a reputation for low prices.

H. Intuitively, we usually think that reputational incentives lead to Pareto superior outcomes. But reputational incentives could actually lead in the opposite direction. Outlaws might try to develop reputations for ferocity, or dictators for brutality.

I. How can the standard intuition be rationalized? Add on free entry and exit. Then people with bad reputations earn no advantage because they have no one to interact with.

1. The Tullock PD-with-partner-selection experiment.

V. Monopoly and Contestability

A. You have all seen the standard monopoly model. The monopolist maximizes PQ-TC, and sets MR=MC.

B. Does this make sense in game theoretic terms? Sure, this is an equilibrium. But there is also an equilibrium where consumers refuse to buy anything if P>MC, so the monopolist sets P=MC. And of course there are many other equilibria.

1. Question: What extra assumptions and/or solution concept underlie the standard account?

C. Still, the standard account intuitively seems right as far as it goes. The main problem is that it neglects potential competition.

D. Contestability models offer one of the most appealing ways to analyze potential competition. Basic setup: An incumbent firm sets its price. Then a potential entrant decides whether to enter and, if so, at what price. Consumers buy from the lower-priced firm.

E. Suppose TC=bQ. Then if P_i>b, the entrant enters and charges P_e= P_i -e, leaving the incumbent with 0 profits. The only NE is where the incumbent charges P_i=b and the entrant stays out.

F. What if the entrant has higher costs than the incumbent? Then the incumbent prices just below the entrant's costs.

G. What if there are fixed costs, so TC=a+bQ? Then P=b is no longer an equilibrium, because that implies profits of -a<0. In that case, the incumbent prices at AC instead of MC.

H. What if there is a sunk cost of a, followed by pricing decisions? Then the first-mover acts like a monopolist, since if entry occurs, both firms will compete price down to b, and both lose money.

I. What about simultaneous decisions to incur sunk costs? Analyze the following normal form.

	In	Out
In	-a, -a	P^m,0
Out	0, P^m	0,0

VI. Allocative versus Productive Inefficiency

A. Most micro texts focus on the allocative inefficiency of monopoly.

A. Main intuition: Landsburg on "Why Taxes Are Bad." Units consumers buy anyway involve only a transfer; units that are no longer bought involve a deadweight loss.

B. Allocative inefficiencies are normally quite tiny, however, because they arise only on the marginal units, or DW loss "triangle."

C. Far less discussed: productive inefficiency. A situation is productively inefficient iff the AC of producing a given quantity is above the minimum AC.

D. Productive inefficiencies can easily be large, because they exist on ALL units produced, yielding a whole DW loss trapezoid.

E. With contestable monopoly and unequal costs, some allocative inefficiency persists, but no productive inefficiency.

F. In contrast, imagine an inefficient monopoly with a price cap at P=MC. There is no allocative inefficiency, but still productive inefficiency.

G. Government-created monopolies versus market monopolies: Both allow for allocative inefficiency, but the former have a strong potential for productive inefficiency as well.

VII. Predation, Entry Deterrence, and Mixed Strategies

A. "Predation" means many things to many people. What insight can game theory shed here?

B. Simplest model of predation: limit pricing. There are many potential producers with varying costs. The lowest-cost producer prices just below the costs of the second-lowest-cost producer, winning the whole market.

1. This probably happens frequently, with or without "predatory intent."

C. More interesting model: Incumbent prices high if no entry, low if entry; entrant decides whether to enter.

D. As discussed earlier, there are two NE: (Out, Fight) and (In, Accommodate). But (Out, Fight) is not subgame perfect. Once the entry happens, the incumbent is better off accommodating. The threat to predate is not credible; the incumbent would be "cutting off his nose to spite his face."

1. Less formal literature emphasizes that predation is especially costly to the incumbent; the game theoretic point is simply that even if predation is cheap, it is more expensive than accommodation.

E. What if predation game is infinitely repeated? Then predation is potentially sustainable. It all depends on the short-term cost of predation versus the long-run monopoly profits. (Here the standard arguments come into their own).

F. Big question about predation: Why can't "two play at that game"? In other words, why can't entrants predate against incumbents just as well as incumbents predate against entrants?

G. Natural solution: Mixed strategy. Returning to the previous normal form, note that in addition to the two PSNE, there is also a MSNE. Potential monopoly profits balance out potential losses of "destructive competition."

H. I maintain that the MS solution makes a lot more sense. There is no way to credibly commit to be In no matter what. The bigger the conditional benefit of being a monopoly, the more willing firms will be to try to win monopoly status.

VIII. Bertrand and Cournot Competition

A. The previous arguments rely heavily on what is known as Bertrand competition (and, to some degree, constant MC). Firms propose prices; all customers buy from the firm that offers the lowest price, and randomize between equal prices.

B. In equilibrium, the most (productively) efficient firm takes the whole market, and charges just below the price of the second-most efficient firm. P=MC if at least two firms can produce in the most productively efficient way.

C. Bertrand competition strongly undermines the perfectly competitive benchmark. It shows that you can get perfectly competitive outcomes with just TWO firms.

D. Perhaps because of this result, many economists prefer the Cournot model of oligopoly. Cournot assumed that firms set quantities rather than prices. The price then independently adjusts to clear the market.

E. Formally, define Q as the sum of all N firms' q's, suppose P=a-bQ, and firms' MC=0. Bertrand competition predicts a price of 0 for all N. What does Cournot predict?

F. Each firm maximizes Pq_i-MCq_i=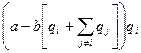. So they set: , which gives the optimal response of firm i given the behavior of all the other firms.

G. Natural solution: Look for the symmetric NE, where all firms produce the same q. Then , so , and .

H. Now Q goes to the perfectly competition level a/b as N goes to infinity. Q falls as N falls even though each firm thinks only of itself and makes no effort to collude.

I. Big weakness of Cournot: Firms would want to split! Under these assumptions, an infinite N would arise endogenously.

J. If you add a fixed cost for each firm, it can also be proven that Cournot competition with free entry is not even second-best. Imposing a zero-profit condition implies an inefficiently large number of firms.

K. Once again, though, if one firm could credibly commit to expand its output and take over the whole market, you would reach the second-best (P=AC) outcome.