Prof. Bryan Caplan

bcaplan@gmu.edu

http://www.bcaplan.com

Econ 812

Week 6: Repeated Games, Competition, and Cooperation, II

I. Bertrand and Cournot Collusion

A. Assuming at least two firms can produce at the minimum MC, the one-shot Bertrand game (as well as the finitely-repeated Bertrand game) has a simple solution: P=MC for all N.

B. In the infinitely repeated Bertrand game, more equilibria are sustainable. What about a perfectly collusive outcome, where each firm produces a 1/N share of the monopoly level of output?

C. As usual, the "trigger strategy" tells us the highest sustainable level of collusion. If one defection leads to a permanent end of collusion, collusive is sustainable so long as a 1/N share of the monopoly profits forever is valued more than 100% of the monopoly profits once, followed by 0 profits thereafter.

D. Formally, the condition is . Simplifying: . The more firms there are, the more each must care about the future for collusion to work.

E. What about Cournot collusion enforced by "Nash reversion" trigger strategies? There are two big differences:

1. Punishments cannot drive profits below the non-cooperative stage game profits. (Makes collusion harder)

2. The defector does not take the whole market. (Makes collusion easier).

F. Formally, the condition is , where P_d indicates defection profits and P_c indicates ordinary Cournot profits. Using last week's functional forms: P_m=a²/4b and P_c=a²/b(N+1)². But how do you calculate P_d?

G. Answer: The collusive/monopoly output level is a/2b. So if all firms other than yourself produce the collusive output level, you simply play your best response to . Thus, you maximize .

H. Differentiating and simplifying: . Then and .

I. Therefore P_d=Pq=.

J. Collusion is therefore sustainable so long as: .

K. Solving for b, we learn that .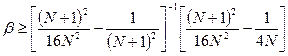

L. If N=2, for example, b*=.53.

M. Remember that these examples abstract from a great many problems with collusion - especially new entry.

II. Public Goods and Game Theory

A. I assume you are all familiar with the concepts of public goods and externalities. While many treatments also emphasize non-rivalry, non-excludability is the key.

A. The basic logic of selfishness:

1. There is no feasible way to exclude non-payers.

2. Since you do not have to pay to use it, selfish people will not pay to use it.

3. And if no one will pay for it, why would selfish producers provide it?

B. Diagramming external costs and benefits.

C. People often use "public goods/bads" and "positive/negative externalities" almost interchangeably. In practice, people tend to call something a public good if private benefits are near-zero, and a public bad if the social benefits are near-zero.

D. It has often been observed that collusion is a public good vis-a-vis the firms in an industry. All firms in the industry would be better off if they all raised prices, but holding the behavior of all other firms fixed, no firm wants to participate.

E. This suggests that provision of public goods can be analyzed using the tools we have already developed for competition and collusion.

F. For starters, we can analyze voluntary donations as a Cournot game. Suppose that individual utility depends on total contributions times personal consumption: U_i=c_iD, where D is the sum of all donations d_i, and c_i+d_i cannot exceed the initial endowment of 1.

G. Looking for the symmetric equilibrium, we learn that c=N/(N+1), whereas utility maximizing c=.5 for all N. Intuitively, as the number of individuals rises, contribution to public goods declines.

1. How come no one contributes to public goods in perfectly competitive settings?

H. This is of course the non-cooperative result. In a repeated game, punishment may sustain higher levels of donation, perhaps even optimal ones. But this requires higher and higher discount levels as the number of players increases.

III. Coase Revisited

A. Coase ("The Problem of Social Cost") famously argued that public goods and externalities problems really boil down to transactions costs problems. With zero transactions costs, people would simply write a contract to get to the cooperative solution.

B. This gives another reason to suspect that degree cooperation declines in N. As the number of transactors rise, presumably so do transactions costs.

C. Still, enforceable contracts allow for cooperation when even trigger strategies are inadequate.

D. In experimental settings, cooperation seems greater than either repeated play or Coase would allow. Presumably this shows that at least some of the time human beings are less selfish than economists assume.

E. Insofar as cooperation arises out of desire to do good, socially harmful collusion seems likely to be less prevalent than socially beneficial cooperation, a point I build on in a paper with Stringham in the RAE.

IV. More on Coordination

A. Recall the simple coordination game:

		Player 2
Player 1		Left	Right
	Left	3,3	0,0
	Right	0,0	5,5

B. In addition to the PSNE discussed earlier, note that there is also a MSNE. However, the MSNE is unstable. If you slip a little bit above or below it, you unravel to an end point.

C. There are many nice applications of Coordination games:

1. Language

2. Culture

3. Technology

4. Location

D. Under the guise of "path dependence," a number of economists have pointed to various forms of inefficient technology lock-in. QWERTY is the classic example.

E. Remember, however, that inefficient lock-in is merely possible. Another possibility is that the status quo is really fine and complaints are "special pleading." Still another possibility, plausible in the case of language, is that while we would be better off if a different language had been chosen long ago, it is not worth changing now.

F. The QWERTY example has been ably debunked in several papers by Margolis and Liebowitz.

G. Coordination problems seem particularly unlikely when the number of players is small, or if there are focal market leaders. Imagine what regulations would have developed if there were dozens of incompatible operating systems!

V. Bargaining

A. Consider this simple model of bargaining:

		Player 2
Player 1		Hard	Soft
	Hard	0,0	5,1
	Soft	1,5	4,4

B. There are two PSNE, but it is the MSNE (.5,.5) that is really interesting. Note further that this MSNE is stable. If 51% of players bargain Hard, your payoff will be higher if you switch your strategy to Soft.

C. Intuition: In equilibrium, both strategies are equally good. As Landsburg says, "Don't mistake a hard bargainer for a good bargainer."

D. Outcome: Not first-best, but the worst outcome only occurs if both sides happen to play Hard (which happens only 25% of the time). As the bad outcome gets worse, fewer and fewer people take the risk of bargaining Hard (though the probability has to remain strictly positive).

E. Of course, people would like you to think they will play Hard. But since everyone wants to be perceived as a Hard bargainer, it is hard to convince anyone that you intend to play Hard.

F. This provides a simple explanation for why people sometimes "stupidly" fail to reach agreement. It could just be bad luck - two Hard bargainers happened to deal with each other.

VI. War and Peace

A. The above bargaining game is better known as the Chicken game or the Hawk/Dove game. It also provides some interesting insight into war and peace (not to mention animal behavior!).

		Player 2
Player 1		War	Peace
	War	-10,-10	5,1
	Peace	1,5	4,4

B. Intuition: Universal peace may be mutually beneficial, but it may be unstable. If all countries are peace-loving, there is an incentive for one country to switch to aggressive bullying.

C. The more horrible warfare is, the less likely any country is to be aggressive, making it very unlikely that TWO countries will be aggressive.

D. Once again, this provides an alternative interpretation of the occurence of wars. The problem may be bad luck (both sides happened to play aggressively) rather than stupidity.

E. How does repeated play affect these results? Peace is certainly sustainable, but another possibility is that countries try to build up reputations for aggressiveness.

F. Hobbes and Leviathan: PD or Hawk/Dove game?

G. One reason why matters aren't worse: Territory/property. Suppose that people are more likely to fight if attacked on their home territory. This expectation makes the threat to fight if attacked more credible than the threat to fight if resisted.

VII. Rent-Seeking and Lobbying Inefficiency

A. We have already discussed allocative and productive inefficiency. A final form of inefficiency is known as lobbying or rent-seeking. inefficiency. It arises when people use resources to effect the transfer of other resources.

B. Simple example: grants of monopoly privilege. Firms pressure the government to become the sole legal producer. The more a firm spends, the better its chances.

C. This lobbying is a sort of "tug-of-war." Bigger prizes induce more effort to win the prize.

D. Gordon Tullock's deep insight: lobbying/rent-seeking is a competitive industry like any other. If lobbying earns a 10% rate of return, and the standard rate is 5%, this will induce "new entry" into the lobbying "business."

E. Note the analogy to mixed strategy reasoning: in equilibrium, the payoffs of production and redistribution must be equal.

F. Firms will keep entering this "arms race" until the net profits of the privilege are zero. This happens when the total costs of lobbying equal the total value of the monopoly privilege! This is known as "full rent dissipation."

1. Can you diagram the "Tullock rectangle"?

G. The government could award monopoly privileges by taking bids (or bribes) rather than listening to lobbyists. But then, Tullock pointed out, this intensifies political competition; if people can get rich in politics, they will pay more to win a seat.

H. This even works in a dictatorship or monarchy; if the dictator can get rich by awarding monopoly privileges, this strengthens the incentives of "upstarts" to try to seize the throne, stage a coup, etc.

I. Once again, repeat play could lead to a better equilibrium, but not necessarily. Firms might lobby extra hard in the hope of acquiring a reputation for toughness.