Economics 812 Midterm
Prof. Bryan Caplan
Spring, 2003
Part 1: True,
False, and Explain
(10 points each - 2
for the right answer, and 8 for the explanation)
State whether each of the following nine propositions is true or false. Using 2-3 sentences AND/OR equations, explain your answer.
Problems 1 and 2 refer to the following information.
1. Agents live for two periods. They are endowed with 1 unit of a consumption good in period 1 and 2 units in period 2. The period 1 good spoils if not consumed in period 1. There are two types of agents:
Type A: 25% of the agents have U=ln c1.
Type B: The other 75% have U=ln c1 + ln c2
True, False, and Explain: The general equilibrium interest rate will exceed 200%.
TRUE. This is just the standard two-good general
equilibrium model applied to intertemporal trade. Thus, we can use the equation from the notes:
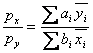 . Specifically:
. Specifically:
![]() . In other words, if you want one more unit of
consumption in period 1, you have to give up 10/3 of a unit in period 2. That means that the interest rate is
233%>200%.
. In other words, if you want one more unit of
consumption in period 1, you have to give up 10/3 of a unit in period 2. That means that the interest rate is
233%>200%.
2. True, False, and Explain: If the two types of agents did not interact (i.e., there is one island for all of the A's and a different island for all of the B's), the interest rate on A would be positive but the interest rate on B would be negative.
FALSE. The interest rate would be positive on both
islands. You do not need to re-do the
calculations to answer. The interest
rate on A would obviously be infinite because the agents put zero value on
period 2 consumption but have positive endowments in that period. But the interest rate on B would also be
positive, because the B's value both goods equally but have bigger endowments
in period 2. Therefore they would seek
to borrow in period 1 until the interest rate got high enough to make them
content to consume 1 unit in period 1 and 2 units in period 2.
3. True, False, and Explain: The Ultimatum Game can
be solved using strict dominance.
FALSE. It can be solved using weak
dominance. Always accepting is a weakly
dominant strategy for the recipient. But
it is not strictly dominant because accepting 0 and rejecting 0 yields the same
outcome.
4. Two players play a Prisoners' Dilemma game followed by a Hawk-Dove game. Consider the following candidate equilibrium: Both players Cooperate in the first game. Then in the second game:
- If both players Cooperated in the first game, both play Dove.
- If one player Cooperated in game 1 and the other didn't, the Cooperator plays Hawk in game 2 and the other player plays Dove.
- If neither Cooperated in turn 1, both players play the MSNE in turn 2.
True, False, and Explain: You need to know the exact payoffs to determine whether this is a subgame perfect NE.
FALSE. It is definitely not a SGPNE. Why not?
Both players playing Dove on turn 2 is not a NE. One player would want to switch to Hawk. This might however be a SGPNE if (Coop, Coop)
in turn 1 led to the MSNE in turn 2.
Then it would depend on the exact payoffs.
Questions 5 and 6 refer to the following information.
Suppose that a store decides whether to cheat or not cheat, and a consumer decides whether to investigate the store's reputation, buy without investigating, or not buy without investigating. Intuitively, if the customer investigates, he is never swindled, but always wastes some time. The cost of investigation is a>0.
|
|
Investigate |
Buy |
Don't Buy |
|
Cheat |
0, -a |
5,-5 |
0,0 |
|
Don't Cheat |
3, 3-a |
3,3 |
0,0 |
5. True, False, and Explain: If a MSNE does not exist, there are two PSNE.
FALSE. If a MSNE does not exist, there is only ONE
PSNE: (Cheat, Don't Buy). A MSNE does
not exist if Investigate is strictly dominated; i.e., if a>5. Once you are left with the two rightmost
columns, it is clear that (Cheat, Buy) is not an equilibrium (the customer
would switch to Don't Buy); (Don't Cheat, Buy) is not an equilibrium (the store
would switch to Cheat); and (Don't Buy, Don't Cheat) is not an equilibrium (the
customer would switch to Buy).
6. True, False, and Explain: If the game is infinitely repeated, the equilibrium (Don't Cheat, Buy) may be sustainable even if a>5.
TRUE. If a>5, it never pays to Investigate. But the customer can still find out about the
store's honesty by buying without investigating and seeing what happens. He could then induce honest behavior with
trigger strategies, for example. Trigger
strategies would work as long as 3/(1-b)³5, where b is the store's discount factor.
7. True, False, and Explain: If firms have heterogeneous costs, the equilibrium in a one-shot Bertrand game will definitely be more allocatively efficient but may be less productively efficient than a one-shot Cournot game.
FALSE. The one-shot Bertrand game is always
perfectly productively efficient, because the lowest-cost producer(s) take over
the whole market. In Cournot, in
contrast, productively inefficient firms may survive. Bertrand games have no allocative
inefficiency if the two most efficient firms are equally efficient, but if
there is a big gap in costs it is possible that allocative inefficiency will be
more severe than in Cournot.
8. True, False, and Explain: Landsburg (Fair Play) argues that leaving childbearing decisions to individuals creates a special kind of Prisoners' Dilemma.
TRUE. But unlike anti-population thinkers,
Landsburg argues that selfishness leads to too FEW children rather than too
many. Families fail to consider the
positive externalities their children will have on the world, and those positive
externalities almost certainly outweigh any negative externalities.
9. True, False, and Explain: Repeated game theory provides a solid theoretical explanation for the widely-accepted view that collusion is more common than predation.
FALSE. Repeated game theory merely shows that in infinitely-repeated
games, both collusion and predation MAY be sustainable. It gives no particular reason to think that
one is more sustainable than the other.
You need more details to understand why predation is less common than
collusion.
Part 2: Short
Answer
(20 points each)
In 4-6 sentences AND/OR equations, answer all three of the following questions.
1. "Journalists seem to think that the costs of foreign
competition can be measured by the number of Americans who leave their jobs as
a result. That's pretty much the
opposite of the truth." (Landsburg, Fair Play)
Use cost-benefit analysis to defend the journalists' position.
The most obvious possibility
Landsburg overlooks is that labor markets don't clear due to downwardly rigid
wages. If so, workers may be randomly
rationed out of their jobs, and unable to find new ones. The workers who stay will be worse off than
those who switch to a new job, but better off than the laid-off.
The journalists might also appeal to positive externalities of work, most obviously those created by the safety net.
2. Explain why the free-entry equilibrium with fixed costs is inefficient in a Cournot game. Is this a realistic prediction? Why or why not? Explain how you would try to break out of this equilibrium if you ran one of the firms.
Take the simplest case where
there is a fixed cost and zero MC. Then
obviously the cheapest way to make a quantity Q is to have one firm make it
all. The social cost is K, versus N*K
for the free-entry equilibrium. Assuming
a homogenous good, however, this prediction is highly unrealistic. One firm could loudly announce that it is
selling for one penny below the price reached by the Cournot auctioneer and
steal the whole market. Cournot
oligopoly would then break down into contestable monopoly.
3. In any long-term friendship, there are multiple equilibria, of which only a small fraction are ever played. Give a good example to illustrate this principle. Building on Kreps' discussion of "Why Might There Be an Obvious Way to Play a Game?" analyze what makes the observed equilibria "special."
There are many ways that
friends could pay for joint restaurant meals: even split, Dutch treat,
alternating full payment, {you pay for one meal, then I pay for two, then you
pay for three...}, and so on ad infinitum.
If your friends expected you to go along with any of these practices,
you probably would. But in practice, the
even split and the Dutch treat are far more common than any other
technique. What makes these equilibria
"special"? Kreps talks about
preplay negotiation, convention, learned behavior, and focal points. Friends rarely negotiate their bill-splitting
system in advance. But convention,
learned behavior, and focal points all probably play a role. I would guess that focal points are the most
crucial: If I ate lunch with a member of an unfamiliar culture, I would still
expect him to expect that we would either split the bill or each pay our own
ways.