Economics 812 Midterm
Prof. Bryan Caplan
Spring, 2004
Part 1: True,
False, and Explain
(10 points each - 2
for the right answer, and 8 for the explanation)
State whether each of the following nine propositions is true or false. Using 2-3 sentences AND/OR equations, explain your answer.
1. Suppose a million
new immigrants enter the
True, False, and Explain: According to Landsburg (Fair Play),
this change usually increases Kaldor-Hicks efficiency, because the positive
effect of population growth on innovation tends to outweigh the negative
externality of falling wages.
FALSE. While Landsburg does discuss the R&D
externalities of population growth, he explains that falling wages are not an
externality at all. It is at worst a
transfer from workers to employers, and if there is any demand elasticity the
fall leads to additional surplus.
Several students also
mentioned that immigration does not necessarily increase world R&D because
one country's population must fall for another's to rise. These answers received a couple extra points.
2. Two types of
agents consume guns (g) and butter (b).
The Type A agents have U=.5 ln g + .5 ln b, and initially own 1 unit of
guns and 1 unit of butter. The Type B
agents have U=.3 ln g + .7 ln b, and initially own .5 units of guns and .5
units of butter. 10% of the agents are
Type A; the other 90% are Type B.
True, False, and Explain: The price of guns will not equal the price of butter.
Plugging into the formula 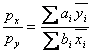 from the notes:
from the notes:
![]() .
.
3. True, False, and Explain: If everyone has lexicographic preferences for x over y, the conclusion
of the First Welfare Theorem holds even though its assumptions do not.
TRUE. With lexicographic preferences, no
equilibrium price vector exists, since if py>0 everyone will want
to sell all they have, and if py=0, everyone will want an infinite
amount. However, any distribution of
resources will be Pareto efficient, because reallocating y or x between people
always leaves one person better off and another person worse off.
4. Consider the following 2-player game:
|
|
Up |
Down |
|
Left |
0,0 |
0,0 |
|
Right |
0,0 |
0,0 |
True, False, and Explain: This game
has 4 PSNE but no MSNE.
FALSE. There are 4 PSNE, but there is also an
infinite number of MSNE. Any probability
mix leaves your opponent indifferent.
(Several students said that there was no reason to randomize, but
that misses the whole point of MSNE. If
neither play can do strictly do better by changing, you have an equilibrium).
Questions 5 and 6 refer to the following information.
Suppose that two players repeatedly play the following game.
|
|
Hawk |
Dove |
|
Hawk |
-10,-10 |
5,0 |
|
Dove |
0,5 |
3,3 |
5. True, False,
and Explain: If the game is repeated
infinitely, trigger strategies can sustain the socially optimal outcome
as long as β>.6
FALSE. The socially optimal outcome (social payoffs
are maximized) occurs at Dove, Dove. The
trigger strategy would be: If you ever play Hawk, I will play Hawk forever
afterwards to punish you, and you will play Dove. It is therefore in a player's interest to
play Dove if:
![]() , which holds as long as b≥.4.
, which holds as long as b≥.4.
Many students assumed that
the cheater would lose 10 every turn, but that would require the cheater to
play Hawk, which he would definitely not do if he expected his opponent to play
Hawk. (Remember – hold all other
player's behavior fixed and see if you can do better solely by changing your
own behavior!) Student who correctly
reasoned from this assumption got 6 points.
A few other students assumed
that the MSNE would be the trigger strategy, but punishing by playing Hawk
forever is obviously a tougher punishment.
If you worked through this approach correctly, you also got 6 points.
6. True, False,
and Explain: If the game is repeated
twice, β=1, and players get to flip a
coin after turn 1, there is no NE where players play (Dove, Dove) in turn 1.
FALSE. I propose the following NE. We both play Dove in turn 1. If we keep this agreement, then in turn 2 we
play (Dove, Hawk) if the coin said Heads, and (Hawk, Dove) if the coin said
Tails. But if player 1 plays Hawk in
turn 1, then in turn 2 we play (Dove, Hawk) regardless of the coin toss, and if
player 2 plays Hawk in turn 1, then in turn 2 we play (Hawk, Dove) regardless
of the coin toss. The payoff from
playing this strategy is 3+.5*5=5.5, which exceeds the payoff from cheating,
which would be 5+0=5.
Incidentally, you could
sustain cooperation even without a coin flip.
Just do the MSNE in turn two if both players played Dove in turn 1. But if player 1 plays Hawk in turn 1, then in
turn 2 we play (Dove, Hawk), and if player 2 plays Hawk in turn 1, then in turn
2 we play (Hawk, Dove). Since both
players play Hawk with p=1/6 in the MSNE, the expected MSNE payoff is once
again:
1/36*-10+5/36*5+5/36*0+25/36*3=2.5.
7. Suppose there is a Cournot industry with the demand function Q=a-bP, 8 firms, 0 MC, and no fixed cost.
True, False, and Explain: A firm
would want to split into two firms because it would earn 62% more profit as a
result.
TRUE. From the hw, we know that profits as a
function of N equals ![]() . So profits for one firm in a industry with 8 firms are
. So profits for one firm in a industry with 8 firms are
![]() , while profits for two firms
in a industry with 9 firms are
, while profits for two firms
in a industry with 9 firms are ![]() . The latter is 62% greater than the former.
. The latter is 62% greater than the former.
8. True, False,
and Explain: Kreps argues that in the "noisy" real world, trigger
strategies are not a practical way to sustain collusion. Instead, colluding firms would only punish if
prices were significantly below the agreed level.
FALSE. Kreps specifically states that "you
cannot go too far in lessening the severity of punishment, making it of shorter
duration, say, or only triggering punishment when prices fall very far. This would encourage each side to chisel
somewhat..." (p.526) Intuition: If
no small deviations get punished, then everyone will always engage in a small
deviation.
9. Suppose firms in
an industry have fixed costs and increasing marginal costs. The industry demand curve lies strictly above
firms' AC curves.
True, False, and Explain: Bertrand
competition will allow only one firm to survive in this market, implying no
productive inefficiency but some allocative inefficiency.
FALSE. With increasing MC, the AC curve eventually
turns up – it will have a U-shape. So if
demand is high, multiple firms can definitely survive. Ignoring divisibility problems, it is
possible for multiple firms to survive in such an industry, setting P=AC=MC.
Part 2: Short
Answer
(20 points each)
In 4-6 sentences AND/OR equations, answer all three of the following questions.
1. "The assumptions of the Arrow-Debreu model are sufficient
but not necessary conditions for the efficiency of laissez-faire."
Discuss this statement, using two specific examples from game theory to illustrate your point.
Arrow-Debreu assumes that
firms have no control over prices. But
in the Bertrand oligopoly game, firms set prices, but can still reach the
first-best outcome where P=MC.
Similarly, in the Ultimatum game, there are no enforceable trades at
all, and yet the game theoretic prediction ($.01 for you, rest for me) is
perfectly efficient. In both cases,
then, laissez-faire is fully efficient even though the A-D assumptions do not
hold.
Other good examples some
students used: repeated play (including reputation), coordination games.
2. Use Tullock's insights on rent-seeking to analyze students' allocation of effort between studying and cheating. What changes if students can bribe professors for better grades?
Tullock would predict that
students would keep cheating until the rate of return from studying equals the
rate of return from cheating. In
equilibrium, both methods of earning grades would have to be equally effective. If students can bribe professors, this leads
students to cut back on both studying and cheating in favor of cash
bribes. On the surface, this seems
clearly more efficient. But there is an
externality on the value of the diploma.
More interestingly, if professors can extract bribes from their
students, this will lead to additional competition for academic jobs (like
getting a second Ph.D.), presumably with little social benefit.
3. Suppose you have a 2-player version of the voluntary donation game from the notes, with one difference: Each agent cares somewhat about the other, so player one maximizes U1=c1D+.5*c2D, and player two maximizes U2=c2D+.5*c1D. Carefully set up each player's maximization problem. Then solve for the symmetric Nash equilibrium.
Note that D=d1+d2=2-c1-c2. So player 1 maximizes:
U1=c1(2-c1-c2)+.5*c2(2-c1-c2)=2c1-c12-1.5c1c2+c2-.5c22
And
player 2 maximizes: U2= 2c2-c22-1.5c1c2+c1-.5c12
Differentiating
U1 wrt c1: 2-2c1-1.5c2=0
Differentiating
U2 wrt c2: 2-2c2-1.5c1=0
Solving
2 equations in two unknowns implies c1=c2=4/7. Each player keeps 4/7 for himself and donates
3/7 to the common fund, whereas in the simple model without altruism, each
agent keeps 2/3 for himself and donates only 1/3. Altruism partially solves the public goods
problem.