Prof. Bryan Caplan

Economics 812 Midterm

Prof. Bryan Caplan

Spring, 2009

Part 1: True, False, and Explain

(10 points each - 2 for the right answer, and 8 for the explanation)

State whether each of the following nine propositions is true or false. Using 2-3 sentences AND/OR equations, explain your answer.

1. True, False, and Explain: In practice, ex ante Pareto efficiency is equivalent to Kaldor-Hicks efficiency, because in the long-run, the benefits of allowing uncompensated Kaldor-Hicks improvements more than cancel out the losses.

FALSE. While many, perhaps most, people will be ex ante better off if you allow uncompensated K-H improvements, in the real world it is still extremely unlikely that everyone will be better off. As I said in the notes, “someone somewhere is sure to slip through the cracks.” As a result, the ex ante Pareto efficiency standard, unlike the Kaldor-Hicks efficiency standard, ends up approving of every status quo.

Problems 2 and 3 refer to the following information.

2. Agents live for two periods. They are endowed with 1 unit of a consumption good in period 1 and 2 units in period 2. The period 1 good spoils if not consumed in period 1. There are two types of agents:

Type A: 10% of the agents have U=ln c₂.

Type B: The other 90% have U=ln c₁ + ln c₂

True, False, and Explain: The general equilibrium interest rate will exceed 200%.

FALSE. Normalize the two utility functions, then apply the formula from the notes to get 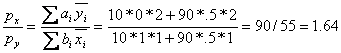, implying a 64% interest rate.

3. True, False, and Explain: If the two types of agents do not interact (i.e., there is one island for all of the A's and a different island for all of the B's), the interest rate on A will be positive but the interest rate on B will be negative.

FALSE. Applying the formula from the notes, we see that on the type A’s island:

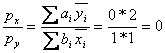, implying a -100% interest rate (not, as many people said, negative infinity!). Intuitively, on the island where no one values consumption in period 1, lending in period 1 consumption buys you nothing in period 2.

Similarly, on the type B’s island:

, implying a 100% interest rate. Intuitively, the type B’s value both kinds of consumption equally, but have a larger endowment in period 2, so they try to borrow against their higher future earnings.

4. Consider the following normal form:

	Left	Right
Left	2,2	0,0
Right	0,0	0,0

True, False, and Explain: This game has one PSNE and one MSNE, but it can be solved through weak dominance.

FALSE. The game has two PSNE: (Left, Left), and (Right, Right). It has no MSNE – if you try to solve for one, you just get “play Right” with 100% probability for both players. The game can however be solved through weak dominance: Left is sometimes better the Right, and never worse.

Problems 5 and 6 refer to the following information.

Kreps imagines a monopolist’s monologue:

Out there are many people who would enter this industry and take away my profits if they thought they that they could themselves make a profit... My choice of an output level of 5 may look silly in the short run, but if it keeps you (and other potential entrants) out of my market, it is a good strategy to employ.

5. True, False, and Explain: Kreps’ monopolist engages in “limit pricing.”

FALSE. The notes explain that “limit pricing” is when the lowest-cost firm sets its price just below the costs of the second-lowest-cost firm. In Kreps’ example, in contrast, firms have equal costs. What Kreps’ monopolist is trying to do is take advantage of its first-mover advantage to make output so high that an entrant would be unable to cover its costs.

6. Kreps adds, “Now rather a lot is wrong with the story just told...”

True, False, and Explain: The monopolist’s story might be OK in a repeated game IF there are also sunk costs.

FALSE. The monopolist’s story can work with repeated play OR sunk costs; either one is enough. With repeated play, a monopolist might endure losses in the hope of deterring future entry. With sunk costs, the monopolist’s first-mover advantage would be stronger – once it locks in its quantity, the entrant would know for sure that it would lose money (rather than convincing the monopolist to reduce its output to accommodate the entrant).

7. Suppose two players play the following normal form N times. N is finite and known by both players.

	Left	Right
Left	5,1	0,0
Right	0,0	1,5

True, False, and Explain: Alternating back and forth between (L,L) and (R,R) is an equilibrium as long as N is even and β≥5/6.

FALSE. This is an equilibrium for all N and all β. Whenever a firm defects from it, it gets 0 instead of 1 or 5, so there’s never any point in deviating.

8. Consider a Cournot model with two firms. P=10-Q, and MC=0.

True, False, and Explain: If one firm moves first, the unique SGPNE has a higher Q than it does with simultaneous play.

TRUE. Applying subgame perfection, let’s start with the second mover. It maximizes:

, implying:

, so

In a SGPNE, the first mover takes the second-mover’s reaction function into account. This means that it substitute’s firm 2’s reaction function into it’s own profit function before taking the derivative:

. This simplifies to:

. Maximizing wrt gives us:

, so . Now plug into firm 2’s reaction function to get:

. Since Cournot output is: , output rises.

BTW, you may already be familiar with this problem as the “Stackelberg model.”

9. True, False, and Explain: The War/Peace game confirms the view that the invention of atomic weapons reduced the risks of war and human extinction.

FALSE. In the MSNE, the probability of playing War falls as the (War, War) payoff gets more negative; and since the probability that (War, War) happens is that [P(War)]², the risk of war goes down. However, the probability of human extinction still probably goes up – nukes make war less likely, but much more devastating if it does happen.

Part 2: Short Answer

(20 points each)

In 4-6 sentences AND/OR equations, answer all three of the following questions.

1. People occasionally argue that Western consumers are virtually “satiated” – before long, they will have everything they want. Assume this claim is correct, and that labor productivity continues to improve. Describe the general equilibrium consequences for output, employment, wages, and real interest rates. Carefully explain your reasoning.

What happens:

Output: Output continues to rise slightly as labor productivity keeps going up, approaching but never reaching the satiation level. If output hit satiation, people would stop working; but otherwise the tendency of greater productivity to raise output remains.

Employment and wages: Increasing labor productivity raises labor demand, and as workers approach satiation, their labor supply curve starts to bend backwards. The result: Wages go up, but employment declines as satiated high-wage workers switch from labor to leisure.

Real Interest Rates: As the intertemporal GE consumption model at the end of the Week 2 notes explains, positive time preference (β<1) and growing income (g>0) guarantee a positive real interest rate. Since the question says, “Labor productivity continues to improve,” there is no reason to say that real interest rates rise; all we can say is that they remain positive.

Note: The question says “virtually satiated,” not “completely satiated”; furthermore, nothing in the question suggests that consumers would remain satiated if there were a drastic fall in output. It is incorrect, then, to claim that output and employment would fall to zero. Even if this were so, though, wages would still go up, because in GE workers earn their marginal product.

Furthermore, no matter what happens to output, there’s no reason to think that real interest rates would fall. If labor productivity is rising, workers who feel almost satiated today should expect to feel even more satiated next year, so interest rates would still be positive!

2. People (including economists) often think that monopolies are productively inefficient. Why, on reflection, would this be strange? What additional assumptions do you need to make the “inefficient monopolies” story internally consistent?

It would be strange for monopolies to be productively inefficient because regardless of how little competition a firm faces, higher costs imply lower profits. Even a monopoly totally protected by the government should still want to minimize costs; otherwise it’s just leaving money on the table. (Many students mentioned potential competition, but that misses this much more fundamental point).

Two good stories about productively inefficient monopoly:

a. Firms have a range of levels of productive efficiency, and the government decides to legally protect a firm that is NOT the most efficient. This could be because the firm best at lobbying the government for help is not the best at actually producing the product.

b. The firm is a monopoly with regulated profits. This gives it an incentive to eliminate the “excess” profits by letting costs rise, rather than cutting prices. Remember the “gold-plating effect”?

3. If Landsburg’s “People Wanted,” (Fair Play) is correct, does Kaldor-Hicks efficiency require the long-run maximization of population? Carefully explain your answer, staying as close as possible to Landsburg’s descriptive claims about the economic consequences of population growth.

Kaldor-Hicks efficiency does NOT require population maximization. Landsburg points to important positive externalities of child creation. However, positive externalities of X do not imply the efficiency of maximizing X! (By analogy, the negative externalities of pollution do not imply the efficiency of a total ban).

In the absence of natalist subsidies, Landsburg thinks that every child is more than worth its social cost (except, he notes, for criminals, welfare recipients, etc.) In his view:

Benefit to Society > Benefit to the Family ³ Cost to the Family » Cost to Society

As you pile on the subsidies, though, the marginal cost to families of caring for more children go up. Eventually you reach the point where the cost to the family of creating another person exceed the benefit to society. There’s no reason to think this point is equivalent to “long-run maximum population.”

You could also argue that eventually population has negative externalities – not “resource depletion” (as Landsburg explains, that’s doesn’t count), but on e.g. air pollution, congestion, or other uncharged impositions upon your fellow man.

The conclusion that K-H efficiency does not imply population maximization is clearly true if you don’t count unconceived people’s “willingness to pay to be conceived.” Even if you did, though, K-H still might not imply population maximization. Consider: If you already felt completely exhausted taking care of 9 kids, the 10^th kid might have to pay you more than his discounted lifetime earnings to induce you to have him, so the cost of his conception exceeds the benefit.