Economics 812 Midterm

Prof. Bryan Caplan

Spring, 2011

 

Part 1: True, False, and Explain

(10 points each - 2 for the right answer, and 8 for the explanation)

State whether each of the following six propositions is true or false.  Using 2-3 sentences AND/OR equations, explain your answer.

 

1.  Two types of agents live for two periods.  In each period, they receive an endowment of perishable consumption goods – storage over time is not possible.  Type A agents have U=ln c1 + ß ln c2; Type B agents have U= ln c1 + ρ ln c2.  Both types of agents are equally numerous and have endowments of 1 in each period.

 

True, False, and Explain: The equilibrium interest rate r equals 2/(ß+ρ).

 

FALSE.  (1+r) equals the price ratio of period 1 consumption to period 2 consumption.  So just normalize the utility functions to be:

 

 and

 

Then apply the 2-good GE formula from lecture:

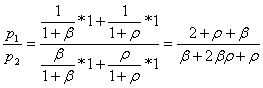.  Since this is equal to (1+r), r=-1,

which does not equal 2/(ß+ρ).

 

 

2.  Consider the following normal form:

 

Left

Right

Left

1,1

0,0

Right

0,0

2,2

 

True, False, and Explain: If two players play this game sequentially, there are three NE but only one SGPNE.

 

FALSE.  Played sequentially, there are only TWO NE (L,L) and (R,R).  The MSNE from the simultaneous version of the game does not exist, because if player 1 randomizes, player 2 gets to see whatever he played, and will therefore copy whatever he did with certainty.  Out of the two NE, only (R,R) is SGP.  You can show this with backwards induction: since player 1 knows that player 2 will match him in the second turn, he always wants to play R.

 

Questions 3 and 4 refer to the following information:

 

An Incumbent and an Entrant infinitely repeat the following game. 

 

Enter

Don’t Enter

Predate

-10,-10

10,0

Don’t Predate

2,2

10,0

 

Consider the candidate equilibrium where the Incumbent always plays Don’t Predate, and the Entrant plays Enter until the Incumbent plays Predate once.  After the Incumbent plays Predate, the Entrant never plays Enter again.

 

 

3. True, False, and Explain:  This is not a NE unless the Incumbent’s discount factor is less than .6.

 

FALSE (but see below).  Playing the candidate equilibrium is Nash if:

.  This simplifies to:

, so .  Since deviating has a short-run cost and a long-run benefit, low discount rates are required to sustain the equilibrium.

 

If you answered TRUE and said the above, I gave you full credit.  Technically, though, since the question says “less than .6” rather than “less than or equal to .6,” the correct answer is FALSE.

 

 

4.  Suppose that every turn, there is a p>0 that the entire industry disappears due to exogenous technological innovation.

 

True, False, and Explain: Predation may still be sustainable.

 

TRUE.  You could interpret β as a continuation probability (1-p) rather than a discount factor and just use the math for Question 3.  Or you just revise the inequality, flip the sign, and solve.  Predation is sustainable as long as:

 

, implying:

 

.

 

5.  True, False, and Explain:  Bertrand competition between identical firms with fixed costs yields a second-best efficient outcome.

 

TRUE.  The first-best outcome is when one firm produces at MC, avoiding any allocative inefficiency from P>MC (the Harberger triangle).  But in Bertrand competition with fixed costs, competition leads one firm to drop out, and the other to set P=AC – a standard second-best result.  At lower prices, firms would lose money and exit.  Bertrand competition will NOT lead to wasteful duplication of fixed costs; if it did, either firm could profit by slightly cutting its price and stealing all its competitors’ customers.

 

 

 

6.  Consider the following one-shot game:

 

Attack

Submit

Defend

Attack

-10,-10

5,-3

-20,-5

Submit

-3,5

0,0

0,-1

Defend

-5,-20

-1,0

-1,-1

 

True, False, and Explain:  There is a MSNE, but no PSNE.

 

FALSE.  Defend is strictly dominated by Submit for both players, so this game simplifies to a standard Hawk/Dove game with the four upper-left cells.  In such games, there are two PSNE – (Attack, Submit) and (Submit, Attack) in this case, plus a MSNE.

 

Part 2: Short Answer

(20 points each)

In 4-6 sentences AND/OR equations, answer all three of the following questions.

 

1.  “People may be unable to articulate, for example, that ‘I would be willing to pay $200 per month in additional rent to live in a safer neighborhood.’ They might even nonsensically assert that ‘You can’t put a price on safety.’ But in acting, they implicitly make such trade-offs.” (Caplan, “Probability, Common Sense, and Realism”)

 

What objection to probability theory is Caplan trying to answer?  Does he succeed?

 

Caplan is answering the objection that probability theory is unrealistic because normal people rarely explicitly calculate probabilities.  He argues that probability is no more unrealistic than the standard assumption that people have a willingness to pay.  Normal people rarely explicitly state their willingness to pay, but their behavior reveals that they still have a willingness to pay.  Similarly, normal people rarely explicitly state their probabilities, but their behavior shows that they have probabilities.  As Caplan writes, “In short, just as demand theory does not commit us to the view that the typical person explicitly ponders, ‘How much Gouda cheese would I buy if the price were a penny per pound? probability theory does not commit us to the view that the typical person explicitly ponders, ‘What is the probability that I have an evil twin?’”

 

2.  Modify the Hawk/Dove game to explain why in the real world – unlike Thomas Hobbes’ Leviathan – two shipwrecked people are unlikely to try to murder each other.  Carefully explain why your model is a good description of the choices and payoffs that human beings would actually face in this situation.

 

The simplest way to modify the Hawk/Dove game is to change the payoffs.  In the real world, (Dove, Dove) is usually more profitable for both parties than (Hawk, Dove) or (Dove, Hawk).  Unilateral aggression could easily lead to the breakdown of trust and cooperation, and require frequent, costly monitoring.  And depending on how “dovish” Dove is, unilateral aggression might even result in some costly injuries for the aggressor as well as the victim.  As a result, Dove becomes a strictly dominant strategy.

 

You could simply keep the usual Hawk/Dove payoffs and model the situation as a repeated game, but then you’d have to explain why repeated play seems likely to lead to cooperation rather than a struggle for dominance.  Focal points, perhaps?

 

3. With full rent dissipation, roughly what would U.S. rent-seeking as a percentage of GDP be?  Is this a reasonable estimate of actual U.S. rent-seeking as a percentage of GDP?  If not, what is the best explanation for the discrepancy?

 

With full rent dissipation, you’d expect U.S. rent-seeking would equal government spending as a percent of GDP, roughly 40%.  This is an unrealistically high estimate; nothing like 40% of GDP is spent on lobbying, however broadly defined.  The best explanation for the discrepancy is that most government spending is NOT up for grabs.  Politicians largely have to satisfy voters to keep their jobs, and voters want money for the elderly, defense, etc., not whoever lobbies the most.  You could also observe that even with full rent dissipation, 40% is an overstatement unless lobbyists are allowed to simply keep their money without offering any costly goods and services in exchange.