Economics 812 Midterm Answer Key

Prof. Bryan Caplan

Spring, 2012

Part 1: True, False, and Explain

(10 points each - 2 for the right answer, and 8 for the explanation)

State whether each of the following six propositions is true or false. Using 2-3 sentences AND/OR equations, explain your answer.

1. Let “CK”=”the results of the Card-Krueger minimum wage study.” Suppose the p(econometrics is reliable)=.8, p(CK|econometrics is reliable)=.3, and p(~CK|econometrics is reliable)=.7.

True, False, and Explain: P(econometrics is reliable|CK)>70%.

FALSE. Using Bayes’ Rule:

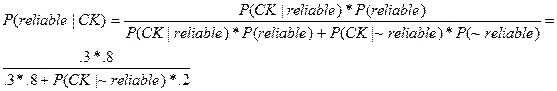
We do not know P(CK|~reliable). But

only if P(CK|~reliable)<.514.

Questions 2 and 3 refer to the following information:

Bryan, Tyler, and John play a game with three possible strategies: Comics, Chess, and Opera. Their payoffs are:

	Bryan	Tyler	John
Everyone Plays Comics	10	1	2
Everyone Plays Chess	1	5	5
Everyone Plays Opera	4	4	4
All Other Cases	0	0	0

2. True, False, and Explain: This game has one PSNE if the players play sequentially, but three PSNE if the players play simultaneously.

FALSE. For the simultaneous game, (Comics, Comics, Comics), (Chess, Chess, Chess), and (Opera, Opera, Opera) are all PSNE equilibria. But so is every situation where each players plays a different strategy: e.g. (Comics, Chess, Opera). This gives everyone zero payoffs, but no individual can increase his payoff by switching. For the sequential game, there is only one subgame perfect PSNE, where the first mover picks the strategy that he most prefers everyone to play – Comics for Bryan, Chess for Tyler or John. But every PSNE in the simultaneous game remains a PSNE in the sequential game.

3. A MSNE also exists.

True, False, and Explain: In this MSNE, Tyler is indifferent when:

P(Bryan plays Comics)*P(John plays Comics)=P(Bryan plays Chess)*P(John plays Chess)=

P(Bryan plays Opera)*P(John plays Opera)

FALSE. This would only be true if all the payoffs for Tyler were equal, which they are not. Tyler is actually indifferent when:

1*P(Bryan plays Comics)*P(John plays Comics)=5*P(Bryan plays Chess)*P(John plays Chess)=

4*P(Bryan plays Opera)*P(John plays Opera)

4. Consider a simple contestable monopoly model where an incumbent faces an equally productively efficient potential entrant. Both have constant marginal costs and zero fixed costs of production. Both firms know that there is a probability p that – if the incumbent remains in business – the government will prosecute the incumbent for antitrust violations. If this occurs, the incumbent loses a fixed cost K. The entrant never faces antitrust prosecution.

True, False, and Explain: Equilibrium quantity is decreasing in both p and K.

TRUE. pK is effectively a fixed cost. Since only the incumbent faces this cost, the entrant will inevitably drive him from the market. The entrant chooses the highest price consistent with driving the incumbent from the market, an epsilon below the point where the incumbent’s AC curve intersects the demand curve. The higher p and K, the higher the incumbent’s AC, and the higher the price the entrant can safety charge.

5. True, False, and Explain: With zero costs of production, Kreps (A Course in Microeconomic Theory) shows that consumers are better off in a Stackelberg equilibrium than a Cournot equilibrium.

TRUE. Kreps shows that under Cournot, total output equals 2(A-k)/3, while under Stackelberg, total output equals 3(A-k)/4. With zero costs of production, k=0, so Cournot output equals 2A/3, while Stackelberg output equals 3A/4.

6. Consider the following one-shot game:

	Attack	Submit
Attack	-1, -1000	100,1
Submit	1,100	50,50

True, False, and Explain: There are two PSNE and one MSNE, but only (Attack, Submit) is focal.

TRUE. This is just the Hawk-Dove game, so (Attack, Submit) and (Submit, Attack) are the two PSNE, and there is also a MSNE. But given the fact that (Attack, Attack) is extremely bad for player 2, (Attack, Submit) is a strong focal point: Both players will look at it and think “Player 2 won’t want to risk attacking.”

Part 2: Short Answer

(20 points each)

In 4-6 sentences AND/OR equations, answer all three of the following questions.

1. Are any of the main assumptions of general equilibrium theory true in the real world? Carefully explain your answer.

The assumptions that there are I consumers, K commodities, non-negative consumption, and endowments are all trivially true; even an endowment vector of all zeros is still an endowment. But none of the other assumptions are empirically true:

a. Utility is not increasing in all commodities, because some people actually dislike some goods and/or reach satiation points.

b. The market price vector is not continuous, because the penny is the smallest unit.

c. Given a price vector, people are sometimes indifferent between different consumption bundles (e.g. blue shirts vs. green shirts), so U_i(p) does not have a unique solution for everyone.

d. There are some goods (e.g. air) where people satiate at price=0, so total demand does not always exceed total endowment for a low enough price.

e. There are lumpy goods and discrete reactions, so the total demand function is not continuous in p_k.

2. Why does popcorn cost more at movies? You should either (a) offer an answer Landsburg fails to consider in The Armchair Economist, or (b) argue that Landsburg prematurely rejects the right answer.

I think Landsburg prematurely rejects the price discrimination story. Yes, there are many theaters, but they are hardly perfect substitutes for each other. Theaters are at best monopolistically competitive. Every theater has a least a mild geographic monopoly; people won’t want to drive an extra 15 minutes to cut the cost of popcorn by a $1. Why price discriminate on popcorn, but not the restrooms? Probably because of fairness norms: Theater goers would be very resentful if they had to pay extra to use the restroom, leading to less repeat business.

3. Compare the maximum deadweight costs of a government grant of monopoly to the deadweight costs of outright prohibition of a product. How would your answer change for a product with negative externalities? Use graphs to clarify your answer.

The worst-case scenario for a government grant of monopoly is when (a) the government gives the grant to a productively inefficient firm, and (b) there is full rent dissipation during the struggle to get the grant. The only social benefit is the triangle of consumer’s surplus under the demand curve and above the monopoly price.

The worst-case scenario for Prohibition is even worse: If the ban is strictly enforced, all the surplus in the market is destroyed.

With negative externalities, however, a grant of monopoly or outright prohibition might actually be the most efficient policy. It depends on the severity of the externalities: You have to compare socially optimal output to output under perfect competition, monopoly, and prohibition. The larger the externality, the more likely monopoly (or even prohibition) will be welfare-enhancing. For small externalities, however, it may be more efficient to have overproduction due to competition than underproduction due to monopoly.