Prof. Bryan Caplan

Economics 812 Midterm Answer Key

Prof. Bryan Caplan

Spring, 2013

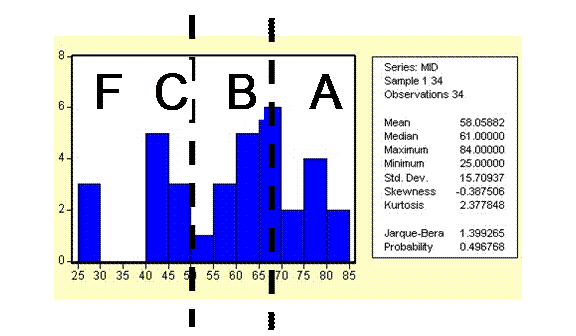
Approximate Grades

67-120 A

50-66 B

40-49 C

0-39 F

Part 1: True, False, and Explain

(10 points each - 2 for the right answer, and 8 for the explanation)

State whether each of the following six propositions is true or false. Using 2-3 sentences AND/OR equations, explain your answer.

1. True, False, and Explain: As population increases, finding real-world Pareto improvements becomes more difficult.

TRUE. A change is only a Pareto improvement if absolutely no one is better off. As population grows, you increase the chance of hurting at least one person, especially since you increase the chance of the existence of a person with misanthropic or otherwise “weird” preferences. Furthermore, as population increases, the cost of identifying and compensating 100% of all losers goes up.

2. Suppose all agents have lexicographic preferences for either X or Y. At least one agent has lexicographic preferences for X over Y, and at least one agent has lexicographic preferences for Y over X. All agents start with X>0 and Y>0.

True, False, and Explain: A unique general equilibrium exists.

TRUE. As long as 0<(p_X/p_Y)<∞, everyone with a lexicographic preference for X will want to sell ALL his Y, and everyone with a lexicographic preference for Y will want to sell ALL his X. But to clear the market, the market value of all the X on the market must equal the market value of all the Y on the market. This happens when p_X*(total X endowments of Y-preferrers)=p_Y*(total Y endowments of X-preferrers); in other words, when

p_X/p_Y=(total Y endowments of X-preferrers)/(total X endowments of Y-preferrers), the unique general equilibrium. For example, if the X-preferrers start with a total of 200 Y, and the Y-preferrers start with a total of 100 X, the unique GE is p_X/p_Y=200/100=2.

3. Consider the following variant on the Ultimatum Game:

		Player 2
Player 1		Accept	Reject
Player 1	t	(10-t),t	0, Z

Z=0 if t≥5, but Z=1 if t<5.

True, False, and Explain: There are an infinite number of PSNE, but only one SGPNE.

TRUE. This is just like the Ultimatum Game in the notes, except that the unique SGPNE is now for Player 1 to offer 1 (I also accepted 1.01 and 1+ε), because Player 2 strictly prefers to Reject offers less than 1. As in the Ultimatum Game in the notes, there are an infinite number of PSNE, because IF Player 1 expects Player 2 to Reject any offer less than X, Player 1’s optimal response is to offer X. In this variant, X can be any number from 1-10.

4. “But once you’re in the theater, the owner has a lot of monopolies.” (Landsburg, The Armchair Economist)

True, False, and Explain: Landsburg’s point is that when monopolies sell a product with multiple features, they tend to reduce quality on all margins - to charge a monopoly price for each and every product feature.

FALSE. Precisely the opposite is true. Landsburg’s point is that monopolists normally want to charge a competitive price on each and every product feature, then charge a monopoly price for the PACKAGE. Otherwise, theater owners would want to charge high prices for the bathrooms and every other amenity in the theater. Landsburg’s conclusion is that monopoly by itself cannot explain high popcorn pricing. A better explanation is price discrimination: If willingness to pay for popcorn positively correlates with willingness to pay for admission, but willingness to pay for bathrooms does not correlates with willingness to pay for admission, then charging more than MC for popcorn makes sense.

5. Consider an infinitely repeated Bertrand game with N equally productively efficient firms with constant MC and 0 fixed cost. The firms want to collude. Their system: each period, the cartel randomly picks one firm (1/N chance per firm) to charge the monopoly price. All the other firms charge the monopoly price + $0.01. The firms enforce this agreement with trigger strategies.

True, False, and Explain: Since all firms expect a 1/Nth share of the monopoly, this equilibrium is sustainable as long as .

FALSE. In any period, a firm that is NOT supposed to charge the monopoly price earns 0 if it sticks to the plan, but earns if it deviates by charging $.01 less than the monopoly price. The expected value of future profits for subsequent periods are , because each firm has a 1-in-N chance of getting to charge the monopoly price and reaping the monopoly profits in each period. To sustain collusion, then, we need:

_. This simplifies to: , implying .

Collusion is harder to sustain in this scenario than when colluding firms evenly divide the monopoly profits every period.

6. True, False, and Explain: Kreps argues that in the "noisy" real world, trigger strategies are not a practical way to sustain collusion. Instead, colluding firms would only punish if prices were significantly below the agreed level.

FALSE. Kreps specifically states that "you cannot go too far in lessening the severity of punishment, making it of shorter duration, say, or only triggering punishment when prices fall very far. This would encourage each side to chisel somewhat..." (p.526) Intuition: If no small deviations get punished, then everyone will always engage in a small deviation.

Part 2: Short Answer

(20 points each)

In 4-6 sentences AND/OR equations, answer all three of the following questions.

1. Caplan (1999, 2001) defends the unrestricted use of subjective probability theory in economics. What is the best objection to his position? State your case as forcefully as possible.

There were several good answers to this question. One was that most people assign discrete probability categories (certain, highly likely, somewhat likely, 50/50, somewhat unlikely, highly unlikely, impossible) rather than 0-1 numbers, and that these categories predict their behavior better than a continuous model. Another was that most people don’t know Bayes’ Rule, and therefore frequently violate subjective probability theory on a very deep level.

2. Suppose artificial intelligence researchers produce and patent a perfect substitute for human labor at zero MC. Use general equilibrium theory to predict the overall economic effects on human welfare before AND after the Artificial Intelligence software patent expires.

While the patent lasts, the patent-holder will produce a monopoly quantity of AIs. As a result, the effective labor supply increases, and wages for human beings fall – but not to 0 because the patent-holder keeps P>MC. The overall effect on human welfare, however, is still positive! Since the AIs produce more stuff, and only humans get to consume, GDP per human goes up. How is this possible if wages fall? Simple: Earnings for NON-labor assets (land, capital, patents, etc.) must go up. Humans who only own labor are worse off, but anyone who owns a home, stocks, etc. experiences offsetting gains.

When the patent expires, this effect becomes even more extreme. With 0 fixed costs, wages fall to MC=0, but total output – and GDP per human – skyrockets. Human owners of land, capital, and other non-labor assets capture 100% of all output. Humans who only have labor to sell, however, will starve without tax-funded redistribution or charity.

3. Suppose you play a 5-turn Centipede Game with (a) a random American, and (b) a random Ph.D. Micro student at GMU. How would you personally play in each of these cases? What percentage of the theoretical maximum payoff would you receive in each case? Explain your answer.

If I played a random American, I would definitely NOT expect him to do backwards induction. I would however expect the random American to cheat on his last turn, so I would cheat one before that. (If I liked the person, or if I were playing a child, I would probably just cooperate the whole way through... depending on the sum at stake).

If I played a random Ph.D. Micro student at GMU, my strategy would heavily depend on anonymity. If the student and I knew or expected to discover each others’ identities, then I would cooperate the whole way through... unless there was a lot of money at stake. If we were anonymous, however, I would expect my opponent to cheat on the round right before my last turn, so I would cheat one round before that. With a 5-turn game, that basically means I would cheat at the first opportunity – but if the game were longer, I would definitely try cooperating until the last five turns or so.