Economics 812 Midterm

Prof. Bryan Caplan

Spring, 2013

 

Part 1: True, False, and Explain

(10 points each - 2 for the right answer, and 8 for the explanation)

State whether each of the following six propositions is true or false.  Using 2-3 sentences AND/OR equations, explain your answer.

 

1.  Suppose the government imposes a tax on air pollution.

 

True, False, and Explain: While this tax doesn’t have to be a Kaldor-Hicks improvement, it remains theoretically possible for it to be a Pareto improvement.

 

TRUE.  The tax doesn’t have to be a Kaldor-Hicks improvement; imposing a very high tax on something with a mild negative externality could easily make total social surplus lower.  (Picture a $1000/day tax for skipping a shower).  Nevertheless, a tax on air pollution can, as a matter of pure theory, be a Pareto improvement.  Each individual could conceivably value the improved air quality more than the tax.

 

[Many students said FALSE, on the grounds that if a change is not a Kaldor-Hicks improvement, it cannot be a Pareto improvement.  But the question said that the change might not be a Kaldor-Hicks improvement.  This merely implies that the change might not be a Pareto improvement, which of course is perfectly compatible with the theoretical possibility that the change is a Pareto improvement.]

 

2. Suppose that two players play this PD game, followed by this Coordination game.

 

 

Defect

Don't

 

 

L

R

Defect

3,3

4,0

 

L

5,5

0,0

Don't

0,4

2,2

 

R

0,0

5,5

 

 

True, False, and Explain: If ß=.9, the only SGPNE are (Defect, Defect), (L,L) and (Defect, Defect), (R, R).

 

[I accepted either of the following responses.]

 

[Response #1: The literal answer.] 

 

FALSE.  The first game isn’t really a PD, because the socially optimal result (Defect, Defect) is strictly dominant.  Both (Defect, Defect), (L,L) and (Defect, Defect), (R,R) are equilibria for ALL values of β.  But there is a third equilibrium: (Defect, Defect) followed by the mixed strategy equilibrium of playing L 50% of the time and R 50% of the time.  Furthermore, this MSNE allows for a strange equilibrium: (Don’t, Don’t), followed by either (L,L) or (R,R) if both players played (Don’t, Don’t) in the first round, or the MSNE if either player played Defect in the first round.  This is an equilibrium as long as:

 

2 + 5β ≥ 4 + 2.5β, implying a critical β=.8.

 

[Response #2: The answer assuming the first game really was a PD, with (Defect, Defect) payoffs of (2,2) and (Don’t, Don’t) payoffs of (3,3)].

 

FALSE.  Both (Defect, Defect), (L,L) and (Defect, Defect), (R,R) are equilibrium for ALL values of β.  But there is another obvious equilibrium: (Defect, Defect) followed by the mixed strategy equilibrium of playing L 50% of the time and R 50% of the time.  This is an equilibrium as long as:

 

3 + 5β ≥ 4 + 2.5β, implying a critical β=.4.

 

3. True, False, and Explain:  In an Ultimatum game, a 50/50 split is the only SGPPSNE; in a Dictator game, a 100/0 split is the only SGPPSNE.

 

FALSE.  In experiments, 50/50 splits are common for both games.  Theoretically, however, the SGPPSNE of the Ultimatum game is (100-ε,ε), where ε is the smallest amount the giver can give.  The giver has no reason to give more because the receiver will always accept anything more than 0.  In the Dictator game, similarly, the SGPPSNE is (100,0) because the Dictator has no incentive to share even a penny.

 

4. “Suppose that a manufacturer does hold an unbreakable patent on a particular product.” (Kreps, A Course in Microeconomic Theory)

 

True, False, and Explain:  Kreps says that firms may engage in entry deterrence even if they have a legal monopoly (such as a patent).

 

TRUE.  Even firms with a legal monopoly have to worry about competition by similar products, giving them an incentive to reduce their prices to discourage entry.  As Kreps explains on p.304, “The scope of patent protection does not always extend to protection against close substitutes for the patented product... Then the monopoly may act in a way to impede the entry of producers of these substitute goods.”

 

5.  Suppose firms in an industry have the same cost function, including a sunk cost.  Product demand falls, leading to a halving of potential monopoly profits.  Two firms play mixed strategies to decide whether to enter.

 

True, False, and Explain:  The probability that both firms enter and lose money falls by a factor of four.

 

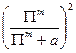FALSE.  From the homework, we know that the probability that ONE firm plays enter is , so the probability that BOTH firms do so is .  Halving monopoly profits reduces the entry probability to .  This clearly reduces the probability of entry, but by LESS than half.  (To halve the probability, the entire denominator, not just part of it, would have to double).  Since the probability that one firm enters falls by less than half, the probability that two firms enter,  , falls by LESS than a factor of four.

 

6.  Suppose N equally efficient firms lobby the government for a monopoly privilege.  The firms never collude.

True, False, and Explain:  Bertrand-style lobbying will lead to a larger Tullock rectangle than Cournot-style lobbying would.

TRUE.  Note that the question specifies Bertrand- or Cournot-style LOBBYING.  The natural interpretation is that with Bertrand-style lobbying, whichever firms lobbies the MOST wins the monopoly for sure, whereas with Cournot-style lobbying, your chance of winning the privilege depends on your lobbying as a fraction of TOTAL lobbying.  By the usual logic, Bertrand lobbying leads one firm to set its lobbying equal to the total value of the monopoly, and all rivals to give up.  Cournot lobbying, in contrast, leads all firms to lobby somewhat, but not enough to wipe out all the profits (i.e., to get full rent dissipation).

 

Part 2: Short Answer

(20 points each)

In 4-6 sentences AND/OR equations, answer all three of the following questions.

 

1. Why doesn’t the First Welfare Theorem imply that market outcomes are Pareto efficient even in the presence of externalities?  Why does Caplan claim that, the First Welfare Theorem notwithstanding, real-world market outcomes are Pareto efficient in the presence of externalities?

 

The no-externalities assumption is implicit in the assumption that Utility Ui(x) solely depends on all K commodities in YOUR consumption bundle.  This means that no consumers’ consumption affects any OTHER consumer’s utility.  With externalities, this assumption is false, so the FWT need not hold.

 

Caplan claims that real-world outcomes are Pareto efficient because (a) any change is almost certain to make SOMEONE worse off, and (b) there is no feasible way to compensate 100% of the losers for any realistic change.  As a result, there is no actual way to make one person better off without making someone else worse off.  As a result, the world is Pareto efficient with or without externalities.

 

 

 

2. Suppose you had to play a 100-turn Hawk/Dove game with one other student in this class.  Before the game starts, you are allowed to send your partner a one-paragraph essay on the theme, “You should cooperate with me because...”  What would your essay say if you wanted to maximize your payoff?  Be as persuasive as possible.

 

Here’s what I propose we do: We play Dove for turns 1-99.  If either of us plays Hawk, we revert to the MSNE for the rest of the game.  On the last turn, we flip a coin: Heads I play Hawk and you play Dove, Tails I play Dove and you play Hawk.

 

You’re probably a fair and honorable person.  If so, I think you’ll agree that my proposal is both fair and honorable, and happily play along.

 

But on the off-chance that you’re not a fair and honorable person, you should still adhere to my proposal.  This isn’t a PD game, so playing Hawk can easily backfire for you even on the turn you play it.  More importantly, my plan has credible punishments.  Once we expect the MSNE, the MSNE is going to happen.  You heard the same lecture I did.  Finally, my proposal elegantly handles the end-game problem.  If we’ve cooperated for turns 1-99, the coin flip maintains cooperation on turn 100.  And you won’t want to betray me on turn 99, because then on turn 100 you’ll get the MSNE payoff instead of a 50% chance of the (Hawk, Dove) payoff and a 50% of the (Dove, Hawk) payoff.

 

In short, decency and self-interest both point in the same direction.  Let’s play!

 

3. Landsburg (“Why Prices Are Good: Smith versus Darwin”) states that, “In biology there is no equivalent of the Invisible Hand.”  Would Landsburg expect there to be an Invisible Hand for culture?  Explain what you think Landsburg would say, then argue that he’s wrong.  (Hint: Remember that cultural practices are often coordination games).

 

Landsburg would almost definitely NOT expect the Invisible Hand to apply.  As he explains in The Armchair Economist, markets achieve a desirable SOCIAL outcome – efficiency – by channeling competition through PRICES.  Competition alone gets you the bloodbath that is natural selection.  Coordination, similarly, can lock-in all sorts of inefficient outcomes.

 

You could argue, however, that cultures compete with each other, mimicking the usual market mechanism.  People who aren’t happy with Amish culture, for example, are free to switch to non-Amish culture.  New entry is possible, too – so if the current menu of cultural choices is unsatisfactory, you can start your own culture.  Cultures, like firms, must pass the market test.