Prof. Bryan Caplan
http://www3.gmu.edu/departments/economics/bcaplan
Econ 816
Spring, 2000
HW#1 Answers
Part 1: Mathematical Problems
1. Romer, problem 9.2.
IS: y=c-ar
LM: m-p=b+hy-ki
a. [Period 0] If m=y=0, then:
0=c-ar and -p=b-ki
So: r=c/a. Since the money supply is constant and there are no trends or shocks of any other sort, pe=0.
Then: i=r+pe=c/a.
Plugging in, -p=b-k(c/a), so p=k(c/a)-b.
b. [Period 2] Now, pe=g. y=0, so the real interest rate remains r=c/a.
i= r+pe=c/a+g.
Now m-p=b-k(c/a+g), and m=2g, so p=2g+k(c/a+g)-b.
c. [Period 1] Since prices are inflexible for 1 period, p1=p0=k(c/a)-b.
In period 1, people know what prices will be in period 2, so
E1[p2]=p2= 2g+k(c/a+g)-b; thus:
pe=E1[p2]-p1= 2g+k(c/a+g)-b-[k(c/a)-b]=(2+k)g
y1=c-ar1, so m1-p1=b+h(c-ar1)-ki1
Note that: i1=r1+(2+k)g; m1=g.
Combining terms, we have 1 equation in 1 unknown:
g-[k(c/a)-b]=b+h(c-ar1)-k[r1+(2+k)g]
Factoring and canceling, -r1[ha+k]=g-k(c/a)-hc+kg(2+k), so:
r1=[hc-kg(2+k)-g+k(c/a)]/[ha+k]
Therefore, i1=[hc-kg(2+k)-g+k(c/a)]/[ha+k] + (2+k)g, which can be re-written as:
i1=[hc-g+k(c/a)+hag(2+k)]/[ha+k]
d. i1-i0=[hc-g+k(c/a)+hag(2+k)]/[ha+k]- c/a=
[hc-g+k(c/a)+hag(2+k)-{hc+k(c/a)}]/[ha+k]= [-g+hag(2+k)]/[ha+k]=
g[(2+k)ah-1)/[ha+k]
Note that the denominator is always positive, so this expression has the same sign as the numerator; further recalling that g>0:
Nominal rate rises if: (2+k)ah>1, falls if (2+k)ah<1, and is constant if (2+k)ah=1.
Thus, the money growth is more likely to reduce nominal rates if the nominal interest-elasticity of money demand is small, the real interest-sensitivity of IS is small, and the income elasticity of money demand is small. Intuitively, if these elasticities are small, then a larger change in nominal rates is necessary to clear the money market (assuming prices can't adjust).
2. Suppose
that 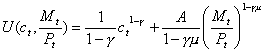 .
.
a. Apply the
formula 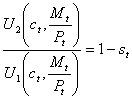 to this particular
utility function to get an equation for money demand as a function of
to this particular
utility function to get an equation for money demand as a function of ![]() .
.
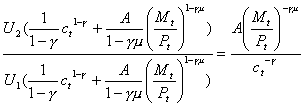
Setting this equal to 1-st:
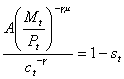
Solving for real money demand:
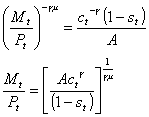
b. Take the log of both sides of the resulting equation. Derive an equation for (log) nominal money holdings as a function of everything else.
Taking logs:
![]()
So:
![]()
c. Does your final equation in (b) make sense?
Yes, nominal log money demand is goes up 1:1 with log prices, is an increasing function of consumption, and a decreasing function of the nominal interest rate. To see the last point, remember that the bigger st is, the smaller 1-st is and the lower nominal interest rates are. So as (1-st) gets smaller, nominal money demanded increases AND nominal interest rates decrease.
Part 2: Analytical Problems
I won't provide sample answers here, but I do have some general and question-specific comments.
Overall: The answers were quite good. Most people actually answered the questions. This is a good technique to remember for the qualifying exams - answer the exact question you've been asked, and move on. Last year, many people just offered general summaries of the concepts mentioned in the question, without actually giving an answer. This is not a good strategy.
1. White: chapter 1, #7
Particularly smart answers observed that even with language, word choice is not arbitrary. Using a twenty-syllable word for fire, for example, would make it more difficult to communicate about fire hazards. So actually, there are sometimes better or worse words, just as there are better or worse monies, and better ones are more likely to be adopted.
2. Is involuntary unemployment a coherent concept? Critique the arguments of one of the following: Lucas, Carmichael, Shapiro and Stiglitz, or Summers (from the week 1 readings).
Answers here were also pretty good. Last year, several people summarized all three positions, without analyzing any of the three.