Prof. Bryan Caplan

bcaplan@gmu.edu

Econ 816

http://www3.gmu.edu/departments/economics/bcaplan

Spring, 2000

I.                     Rational Expectations: What It Is, What It Isn't

A.                 The RE assumption is a critical addition to basic micro.  It is probably the first formalization of the link between economic actors' beliefs and the real world.  (And without such a link, what does economics amount to?)

B.                 Simple characterization: A person has RE if judgments are unbiased (mean error is zero) and mistakes are uncorrelated with "available" information.

1.                  Danger of tautology?

C.                Deeper characterization: A person has RE if his subjective probability distribution is identical to the objective probability distribution.

1.                  Paradox of measurement error in a deterministic world?

D.                Standard modeling technique: everyone is unbiased; information or lack thereof just changes estimates' variance.

E.                 RE in no way rules out error; it does not assume that information or cognition is free.  It just requires that given the information they actually possess (a margin which they also presumably optimize over a la Stigler), they satisfy RE.

1.                  Lucas: "To ask why the monetary theorists of the 1940's did not make use of the contingent-claim view of equilibrium is, it seems to me, like asking why Hannibal did not use tanks against the Romans instead of elephants.  There is no reason to view our ability to think as being any less limited by available technology than is our ability to act (if indeed, this distinction can be defended)."

F.                 RE does treat all uncertainty as quantifiable in terms of probability theory.  But what's wrong with that? 

1.                  Some people feel that somehow in the RE view the uncertain world is still "really" certain.  (Austrian complaint).  E.g.: distinction between "structural" and "parametric" uncertainty.

2.                  My view: since the parameters can be anything - however general - it's far from clear what structural uncertainty is supposed to be, and even less clear that it is ever instantiated.

II.                   RE and Perfect Foresight Equilibria

A.                 A polar case of RE: estimate variance equals 0; i.e., there is no uncertainty: actors know exactly what is going to happen, and choose their responses accordingly.  You have a perfect foresight equilibrium when everyone knows the whole future and plans for it optimally.

B.                 Contrast between RE and perfect foresight equilibria: with RE, people are right on average.  E(P_e)=P.  With perfect foresight, people are right, period: P_e=P.

C.                Note: The simple money demand model from Week 3 was implicitly a perfect foresight model.

1.                  What is your optimal response to a given pattern of money supply growth rates?

2.                  Are your responses over time sharp or smooth? 

3.                  What is the difference between a world where only you have perfect foresight, and a world where everyone has perfect foresight?

III.                  Solving a RE Model: A Simple Macroeconomy

A.                 Adding uncertainty complicates matters, but the extra insight is worth the effort. 

B.                 People can have both nominal and real uncertainties, so both NK and RBC models can and do apply these techniques.

C.                A popular way of solving RE models is known as the "method of undetermined coefficients." 

D.                (You should remember this from your discussion of the Lucas island model, so I include details in these notes solely for review purposes - we won't actually go over them step by step in class).

E.                 Standard Lucas model described by these 5 equations.  All variables are logs of their level values.  y is output, p is the price level, m is the money supply, r is the real interest rate, i is the nominal rate, and u, v, and j are random variables with mean 0.

1.                  (IS)  y_t=x-ar_t+u_t

2.                  (LM) m_t-p_t=by_t-ci_t+v_t

3.                  (Fisher equation) i_t=r_t+E_t(p_t+1)-p_t

4.                  (AS) y_t=y*+a(p_t-E_t(p_t))

5.                  m_t=m_t-1+j_t

F.                 Assume for simplicity that x=0 and y*=0.  Then combine (1)-(4) to find: 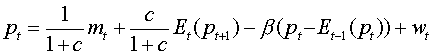 , where  and .

G.                How do you solve this system? 

1.                  Assume that all expectations are rational - i.e., with 0 mean error.

2.                  Then, conjecture the form of the solution.  It would make sense if the price level were a function of the money supply and the random shocks:  .  Note that these coefficients are "undetermined": we don't yet know what they are.

3.                  (Note further that we assumed away trend growth; if there were trend growth, then presumably the price level would be a function of the money stock, random shocks, and the trends).

H.                 Now, apply the expectations operator to the conjectured equation for p_t:

1.                  Lead the equation one period, plug in m_t for E_t(m_t+1), and take the expectations at time t: . 

2.                  Take the expectation of the equation at time (t-1), then substitute m_t-j_t for m_t-1:   Then

I.                     Substitute in for the expectations.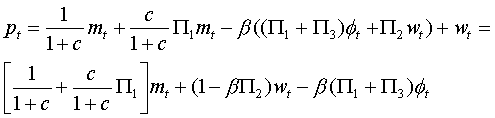

J.                  Now notice: we have two equations for p as a function of m, w, and j.  So set the coefficients on both m's equal to each other, both w's coefficients equal to each other, and both j's coefficients equal to each other.

1.                  , so .

2.                  , so .

3.                  , so . 

K.                 The RE assumption has now led to a simple solution to this system of equations:

L.                  For prices: 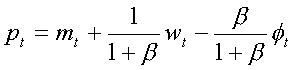.  The price level is directly proportional to the money supply, a positive function of investment shocks, a negative function of money demand shocks, and a negative function of unexpected money supply increases.  (Note that increasing both m and j by 1 still has a positive impact on prices, but less than proportional).

M.                Noting that 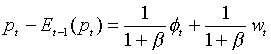, the equation for output can also be derived: 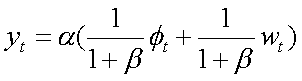.  Output is an increasing function not of money, but of unexpected money shocks; IS and LM shocks also have the standard impact.

N.                 Re-interpret y as employment rather than output; then the preceding analysis gives you the short-run and the long-run Phillips curve (just do simple substitution to go from employment to unemployment).

IV.               Rational Expectations in the Aggregate (Haltiwanger and Waldman 1989)

A.                 H&W distinguish standard RE, where each individual satisfies the RE assumption (which is what most formal models say), and "RE in the aggregate," where everyone's systematic biases balanced out (which is what informal defenses of RE say).

B.                 But in fact, RE in the aggregate often has different implications than standard RE.

C.                Key intuitions:

1.                  With congestion, arbitrage-type behavior by less biased agents dampens social impact of behavior of more biased agents.  Ex: Labor markets, traffic jams.

2.                  With synergy, arbitrage-type behavior by less biased agents amplifies social impact of behavior of more biased agents.  Ex: Technology choice.

D.                Macro implications?

V.                 Was there a RE revolution?

A.                 Wittman’s strange claim.

B.                 Dominant view: RE as a methodological, not substantive revolution.

C.                Minority view: RE is largely confirmed.

D.                Third view: Economic theory offers insight into the limits of RE.

VI.               Alternatives to Rational Expectations, I: Fremling and Lott's "Bias Toward Zero in Aggregate Perceptions"

A.                 Look at agents as implicit econometricians.  Estimation has two stages:

1.                  Setting up your specification.

2.                  Estimating the specification you set up.

B.                 Simple way to relax RE: Assume agents estimate models without bias, but do not necessarily pick the right model.  In particular, faced with an infinite range of variables, they may omit something important.

1.                  What is the econometric impact of omitting a variable?  Logically, it is equivalent to forcing its coefficient to equal zero.

C.                Suppose there are N individuals and k of these include variable X with coefficient b in their implicit model.  Then aggregating over all people, the average estimate = (b*k+0*(n-k))=b*(k/n), which is biased.

1.                  Question: When does the average estimate matter?  With  sufficiently strong congestion in H&W's sense, it may not.  But with synergies (or even zero congestion), this bias can matter a lot.

D.                Note: Even with a relatively small number of variables, the number of possible models increases rapidly.  Over a billion possible causal interactions with just 6 variables.

E.                 A lot of models rejected on RE grounds may make sense according to Fremling and Lott.  You just need a fraction of the population to omit some critical variable.

F.                 Applications:

1.                  Labor markets - no arbitrage to take advantage of each worker's small loss from misspecification.  "Unless money supply shocks have been particularly large, we cannot expect workers to focus on the money stock to the exclusion of other variables."  (Does this refute the $.25 refutation of Lucas island model?)

2.                  Public choice: Political business cycle, price controls, "populism" in general.

G.                My main critiques:

1.                  Media and politicians can enormously whittle down the number of alternative hypotheses.  In F&L, "All news is good news."

2.                  On many issues like price controls, many people will violently resist the standard economic explanation even after they hear it. 

VII.              Alternatives to Rational Expectations, II: "Rational Ignorance vs. Rational Irrationality"

A.                 The puzzle: Low-information, high certainty, systematically biased beliefs.  (Examples)

B.                 My model: People trade off irrationality for wealth.  They do (on some level) perceive the budget line without bias.  On the deepest level, people do have RE.  But if they have a taste for irrationality they will in fact choose to be less than fully rational.

1.                  Interpreting choice over beliefs.

C.                For many beliefs, the budget line is vertical, so people pick their "bliss" belief.  As the budget line gets flatter, people buy less irrationality.

D.                Compare: Neoclassical, near-neoclassical, near-behavioral, and behavioral indifference curves.

E.                 The social cost of beliefs can be quite different from the private cost.  Consider the following cases:

1.                  Choosing religious or political beliefs.

2.                  A worker thinking about his best response to a 1% increase in inflation.

3.                  An employer thinking about his best response to a 1% increase in inflation.

4.                  An arbitrageur thinking about his best response to a 1% increase in inflation.

5.                  Others?

F.                 As H&W implies, it is important to distinguish between:

1.                  Marginal gain from RE when everyone else has RE.

2.                  Marginal gain from RE when no one else has RE.

G.                Any anomalous cases, where benefits foregone are high, but people still don't have RE?

H.                 Rational irrationality illustrated: "Systematically Biased Beliefs About Economics."

1.                  SAEE permits careful comparison of general public and economists, holding all other variables constant.

2.                  Enormous difference in average beliefs revealed by huge coefficients on Econ dummy.

3.                  Controlling for self-serving bias only mildly reduces the size of the Econ coefficient.

4.                  Controlling for ideological bias if anything magnifies the size of the Econ coefficient.

5.                  Controlling for self-serving bias, ideological bias, demographics, and education, large Econ coefficient persists.  Education is also very important however.

6.                  My interpretation: Education and economic training make people "more rational" in the RE sense of the term.  Errors of the economically illiterate are systematic, not random.