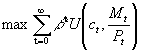bcaplan@gmu.edu

1. Brief Survey of the Course
1. Two main aims:
1. Survey broad range of contemporary topics
2. Focus attention on topics where GMU students have a comparative advantage in the production of new research
2. Main topics to be covered:
1. Microanalytics of money (money supply, money demand, RE)
2. Theory of banking and credit markets
3. Central banking, endogenous and exogenous
4. Privatization of money
5. Great Depression and European unemployment
3. A point of pedagogy: Mathematics and the Laffer curve
2. Money in the utility function
1. Individuals must allocate their wealth between current consumption, future consumption, and their cash balances. So this looks like a standard constrained optimization problem.
2. But, there is a key difference: unlike consumption and investment, money is normally valued for its purchasing power, not for its quantity alone.
1. Ex: How many drachmas do you want to hold when you're in Greece? You have no idea until you find out the real value of a drachma.
3. (Aside: There was a period c.1900 when some economists argued that this prevented the application of marginal utility analysis to money, on account of circularity. Mises is believed by some to have solved the circularity problem with his "regression theorem"; most others have just ignored the problem. But whether or not there is a circularity problem, it is a problem for price level determination, not money demand. The money demand curve just says how much money will be held at all possible price levels, without explaining how those price levels are actually determined).
4. In short, what people want is real money, not nominal money. In consequence, a price of money has to appear in the utility function - as it normally would not. (Of course, prices do normally appear in the indirect utility function).
3. A Simple Model of Money Demand
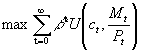1. Objective function: ; an infinitely-lived agent derives utility from consumption and real balances.
2. Agents can consume their wealth, hold it as money, or invest it in bonds. Bonds sell for s_t and pay 1 next period. (They could also just hold real goods between periods, but since real goods pay no interest and give no utility unless consumed, this would make no sense).
3. Budget constraint: ; consumption thing period must equal the agent's per-period endowment (W) plus the agent's transfer from the government (TR - note: this can be negative, i.e., a tax) plus the real value of bonds purchased last period, minus the current real value of bonds purchased this period, minus additions to his cash balance.
4. Note the important assumption that money earns no interest. The present value of consumption equals the present value of endowments less the present value of interest lost as a result of holding non-interest-bearing money.
5. It is intuitively clear that agents will equalize marginal utility along their 3 margins; it will be impossible to increase utility by re-allocating between consumption, bonds, and money. (But note: Bonds are only valued as a means of future consumption).
6. More formally, we can set up the so-called Bellman equation, which just says that we can maximize our lifetime utility by simply maximizing today's utility plus our lifetime utility tomorrow:
7. Taking first derivatives (the argument is indicated by the numerical subscript) and doing a little more work, we can derive two optimality conditions:
8. The first equation just says that you can't gain in utility by buying or selling bonds to shift consumption between present and future. The second equation basically says that you can't gain in utility by swapping current consumption for money.
4. Factors Affecting Money Demand
1. Assume a closed economy so net supply of bonds is zero, consumption equals endowments. Assume further that all transfers are financed by printing money, so , and that transfers are proportional to pre-existing real balances, so . This implies a constant money growth rate of .
2. Note further the (definitional) relationship between the nominal interest rate i and the bond price s: .
3. You can re-arrange the above equations to find that: . When the nominal interest rate rises, 1-s by definition rises, so U₂ must rise and U₁ must fall. From the principle of diminishing MU, this means that when the nominal interest rate rises, agents want to hold less money.
4. In a real economy with fixed endowments, the real interest rate has to be just the inverse of the discount factor, .
5. Since nominal money grows at a constant rate, and real money balances are constant under constant conditions, it follows that the inflation rate must be exactly equal to the money growth rate: .
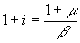6. The nominal rate follows immediately from the real rate and the inflation rate: . It then follows that real money demand falls when the rate of money creation rises, AND when the discount factor falls (i.e., people get more impatient).
7. Price level. Immediate conclusion from the above analysis: Nominal money demand is precisely proportional to the price level, since real money demand is independent of the price level (though not the inflation rate!).
1. N.B. It is a standard micro conclusion that e.g. doubling income and all prices leaves the optimal allocations unchanged. This conclusion is stronger: doubling the supply of just one good leaves both arguments in the utility function unchanged.
8. Real income and real wealth. It can be easily derived from the above model (relaxing the assumption of constant endowments) that so long as money is a normal good, you will hold more in real balances as your real income and real wealth rise.
9. Substitute assets. Take bonds away - then the only way to do inter-temporal substitution is with money. Money demand will rise when there are fewer substitutes for money, and fall when there are more substitutes.
10. Substitute transactions technology. Since it is costly to hold money, alternate means of doing transactions (e.g. credit cards) will reduce money demand. Or changes in the technology of transactions themselves could affect money demand - e.g. cheaper cars means fewer trips to the store, making it more convenient to hold less money. This isn't explicitly in the model, but you could just add a parameter in front of real balances to capture the quality of substitute transactions technology.
11. Others?
5. Circularity, or Coordination?
1. Even if their were a circularity problem with price level determination, you could still figure out your real money demand. But as the above section makes clear, once you've got the real money demand function, you can quickly derive what the price level has to be for a given money supply. How is this possible?
2. Suppose all dollars disappeared. Could I just pass out play money, and derive the value of play money by figuring out what price level is consistent with your former level of real balances?
3. What if we were on a spaceship that crash-landed on a new planet with unknown production possibilities? Would a dollar-based monetary system break down before the spaceship doors open, just because we no longer have any idea what the real value of our nominal dollar holdings is?
4. The problem is not circularity, but coordination. The problem isn't that there is no way to figure out what the equilibrium price level would be if a new money were introduced; the problem is getting everyone to make a "joint deviation" to a new money. Any credible way of doing this works, whether it's:
1. An historically-evolved money.
2. An old fiat money.
3. A new fiat money tied to some real good.
4. A new fiat money that is "focal."
5. This coordination aspect of money means that sub-optimal monetary systems are possible, so it makes sense to deliberate over the advantages and disadvantages of different conceivable monetary regimes (as will be done throughout the course).
6. The Equation of Exchange
1. Famous identity: MV=PY. Like all identities, it says nothing about causality unless you make more assumptions, but it can still be a good way to organize thought.
2. M is money - measured however you like it.
3. PY is nominal GDP; Y is real GDP, and P is the price level.
4. V, velocity, is the number that makes the equation true; its value depends on your choice of monetary aggregate. (V1 is velocity for M1, etc.) V is only "turnover" in a world with no resales.
5. What's your personal V1? V2? What does your personal velocity look like over time?
7. Velocity, Money Demand, and More
1. Velocity is just the inverse of the percentage of your income that you keep in the form of cash.
2. One interesting way to think about velocity: income-adjusted money demanded.
3. If money demand increases/decreases, what happens to velocity? If nominal interest rates rise/fall?
4. Constant V implies that only M matters for nominal GDP.
1. If V is constant, then fiscal policy makes no difference for nominal output.
5. Constant P implies that increases in money or velocity increase real output.
6. Constant Y implies that increases in money or velocity increase the price level.
7. Constant M means that only V matters for nominal GDP determination.
8. Fun fact: V2 has in fact been nearly constant at around 1.7 from early '50's to 1991. V1 much more unstable - large rise to mid-80's, followed by decline.
1. Question: Why did V1 rise for so long, and then fall? Hint: Inflation and regulated interest rates.
8. Cash-in-Advance Models of Money Demand
1. Some people think that it doesn't make sense to put money in the utility function: people want money for what it will buy, not as a final good.
2. Alternate modeling strategy: "cash-in-advance" models. These get essentially the same results as models with money in the utility function.
3. Skeletal cash-in-advance model, using same notation as before. Objective function removes real balances, leaving only consumption: .
4. Constraints change. There is the cash-in-advance constraint that this period's purchases of consumption and bonds cannot exceed this period's money holdings (you need money to buy stuff; barter and autarky assumed away): . There is also a similar second constraint, that next period's money holdings equal this period's sales of endowment and bonds: . Then just maximize O.F. subject to both constraints.
5. All of the standard results work. The only unusual feature is that depending on timing assumptions, you can get a short-run "liquidity effect" - i.e., within a period, a burst of new money reduces real interest rates. Somewhat interesting, since this model has fully flexible prices (but not fully flexible portfolios - they take a period to adjust).
6. My judgment: cash-in-advance adds much more complexity without changing conclusions. Money in the utility function seems like a better approach to me.