Prof. Bryan Caplan
bcaplan@gmu.edu
http://www3.gmu.edu/departments/economics/bcaplan
Econ 918
Spring, 1998
Week 3: The Quantity Theory of Money
- Digression on Nominal Interest Rates and Money Demand
- In terms of the equation of exchange MV=PY, it is generally thought that interest rate changes dampen fluctuations in M.
- An increase in M reduces nominal rates, causing V to fall somewhat since people take advantage of the lower nominal rates to hold more money.
- A decrease in M raises nominal rates, causing V to rise somewhat since people take advantage of the higher nominal rates to hold less money.
- Note however that the postulated co-movement between money and interest rates is the reverse of what the simple theory of money demand tells you. It predicts that increasing the rate of money growth immediately raises nominal rates rather than reducing them.
- So the simple theory of money demand suggests that V amplifies moves in M. Increasing the rate of growth of M makes it more expensive to hold money, raising V as well; cutting the rate of growth of M makes it cheaper to hold money, reducing V at the same time.
- The simple theory is a poor theory for explaining daily interest rate movements. But it seems to accurately describe longer-run situations - in which money creation or destruction has had a certain growth rate for a reasonably long period.
- Hyperinflations
- Sharp deflations
- What is the Quantity Theory of Money?
- The pure theory of money demand provides some interesting insights that canít be mechanically inferred from demand theory generally:
- A one-shot increase in the supply of nominal money raises prices by an equal percent.
- So long as inflation rates are incorporated into nominal interest rates, the nominal interest rate is the key factor for real money demand.
- But: the theory is still general enough to be compatible with a wide range of possibilities.
- The "Quantity Theory of Money," at least as I will use the phrase, is much more specific. (Similar to Sargent-Wallaceís "Unpleasant Monetarist Arithmetic.") According to QTMTM, there exists some stable measure of the money supply such that:
- The sensitivity of money demand to interest rates is approximately zero.
- The sensitivity of money demand to income changes has unit elasticity, or at least is very stable.
- In consequence, you can make quite precise predictions of nominal GDP knowing only the quantity of money.
- N.B.: So long as this holds for any measure of the money supply, broad or narrow, it is stipulated that QTM is true.
- The Quantity Theory as a Theory of Money Demand
- Why might the QTM be true?
- Under normal conditions, the nominal interest rate is fairly low, and the quantity of non-interest-bearing base money is small, so it might not pay much to adjust money holdings in response to interest rates. Base money may be a good like salt - fluctuations in the price of a good that is a tiny fraction of your wealth can make low elasticity optimal.
- Have you ever adjusted your currency holdings due to nominal interest rate fluctuations?
- The interest-rate sensitivity of money demand: with unregulated interest rates, everything except for the monetary base will pay interest. So even if people are sensitive to interest rate changes, these may only cause movements from base money to interest-bearing checking or savings.
- Itís harder to provide a priori reasons for why the income elasticity of money demand would be unitary. But freedom to pick our preferred measure of M makes it easier to satisfy this condition...
- The Quantity Theory as a Theory of Velocity
- If the QTM as defined above is true, then velocity in the equation MV=PY will be constant.
- Intuitively, if money demand has unit-elasticity, and if money demand is insensitive to interest rates, then velocity is likely to be constant.
- This enables you to make quite precise predictions about PY knowing M, especially since weíve assumed away most of the possible sources of endogeneity of M (e.g. M canít be a response to money demand shifts if money demand is extremely stable).
- Note: QTM as defined above is consistent with many kinds of non-neutralities. Itís just a theory of nominal income, not real income.
- Empirical Performance of QTM
- QTM makes very strong claims and precise predictions, especially if you limit discretion about the choice of the "correct" monetary aggregate.
- For a number of decades, researchers focused mostly on M1. The QTM is clearly false for M1: V1 fluctuated greatly just in the U.S. since WWII, and seems to track interest rate changes fairly closely.
- But gradually it was pointed out more and more forcefully that M2 is a far better choice to consider. V2 fluctuates a little bit, but has no clear trend, hovering around 1.7. This continued to hold true even during the Ď80ís as much of the economics profession gave up on the idea of stable money demand functions.
- In short: at least for the U.S. from 1950-1991, the QTM seems to have "worked" better than almost any other quantitative economic law.
- P* Models
- P* models are a pretty straightforward offshoot of the QTM, using a theoretically-derived estimate of the long-run equilibrium price level in order to forecast short-run price movements. Hallman, Porter, and Small (1991) is a good example of this approach.
- P* is defined as the price level consistent with constant long-run velocity, potential real GDP, and M2:
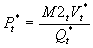 . For the post-war period, HPS just use the sample mean of V2=1.65 (see the QTM connection?), so
. For the post-war period, HPS just use the sample mean of V2=1.65 (see the QTM connection?), so 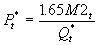 .
.
- Note their long-run graphs, showing that pre-war velocity was anything but constant. Explanations?
- The theory claims that the actual price level P gradually moves to equal P*. On annual data, the ad hoc use of last yearís inflation as a proxy for inflationary expectations yields:
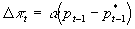 .
.
- Empirical setup: using quarterly data for the U.S. for 1955-88.
- Price-gap equation: works well. Compare to the mean errors and root-mean-squared forecast errors of a number of other models (tables 3-4).
- What can be done to explain the poor performance of P*-models prior to 1950?
- Bordo/Jonung measure: add % labor force not employed in agriculture (and its square). Note that this is a pretty clean explanation, since the non-agro-sector was able to fall greatly for a long time, but gradually began to near its lower bound by 1950.
- "Shift" dummy turns on beginning in 1954. (No explanation).
- Using fitted values for velocity from B-J findings yields results consistent with P*. (Also needed "WWI" dummy for 1917-1921 to make model work).
- Conclusions:
- P* ties together levels of (M&P) as well as growth rates.
- Accumulated growth in M will eventually raise P in spite of short-run inertia.
- HPS published in 1991. Since then V2 has become unstable! The low for V2 from 1960-88 was 1.50; the high was 1.69; yet suddenly:
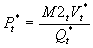 . For the post-war period, HPS just use the sample mean of V2=1.65 (see the QTM connection?), so
. For the post-war period, HPS just use the sample mean of V2=1.65 (see the QTM connection?), so 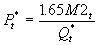 .
. 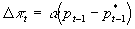 .
.