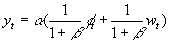Prof. Bryan Caplan
bcaplan@gmu.edu
http://www3.gmu.edu/departments/economics/bcaplan
Econ 918
Spring, 1998
Week 4: Rational Expectations and Money
- Was there a RE revolution?
- Wittman’s strange claim.
- Dominant view: RE as a methodological, not substantive revolution.
- Minority view #1: RE is largely confirmed.
- My view: need a theory of when RE holds as a function of the price of failing to have RE. And to figure out the price, we need to know the RE answer.
- RE and Perfect Foresight Equilibria
- Suppose that there is no uncertainty: actors know exactly what is going to happen, and choose their responses accordingly. You have a perfect foresight equilibrium when everyone knows the whole future and plans for it optimally.
- Ex: with perfect foresight:
- What is your optimal response to a given pattern of money supply growth rates?
- Are your responses over time sharp or smooth?
- What is the difference between a world where only you have perfect foresight, and a world where everyone has perfect foresight?
- Contrast between RE and perfect foresight equilibria: with RE, people are right on average. E(Pe)=P. With perfect foresight, people are right, period: Pe=P.
- Some people have philosophical problems with this move from a world of certainty to a world of uncertainty, feeling that somehow the uncertain world is still "really" certain. (Austrian complaint). E.g.: distinction between "structural" and "parametric" uncertainty.
- My view: since the parameters can be anything - however general - it's far from clear what structural uncertainty is supposed to be, and even less clear that it is ever instantiated.
- Solving a Perfect Foresight Model: Barro&Gordon's Model of Monetary Policy and the Phillips Curve
- The unemployment rate equals the natural rate exceptionally, but is a decreasing function of unanticipated inflation:
 .
.
- Policy-maker has "opportunistic" OF:
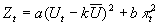 . Note k<1, so the policy-maker wants to push the unemployment rate below the natural rate.
. Note k<1, so the policy-maker wants to push the unemployment rate below the natural rate.
- Two steps to solve:
- First, assume policy-maker maximizes Z in each period, taking into account the impact of (unexpected) inflation on unemployment.
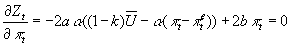
- Set expected inflation equal to actual inflation, since there are no random variables in this equation.
- Therefore,
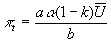 , yet
, yet 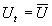
! With RE and no random variables, unemployment always equals its natural rate, yet inflation is well above zero due to the temptation to use policy to reduce unemployment.
- Solving a RE Model: A Simple Macroeconomy
- Adding in uncertainty complicates matters, but the extra insight is worth the effort. A popular way of solving RE models is known as the "method of undetermined coefficients." We'll try it out on a simple example.
- Consider an economy described by 5 equations. All variables are logs of their level values. y is output, p is the price level, m is the money supply, r is the real interest rate, i is the nominal rate, and u, v, and j
are random variables with mean 0.
- (IS) yt=x-art+ut
- (LM) mt-pt=byt-cit+vt
- (Fisher equation) it=rt+Et(pt+1)-pt
- (AS) yt=y*+a
(pt-Et(pt))
- mt=mt-1+j
t
- Assume for simplicity that x=0 and y*=0. Then combine (1)-(4) to find:
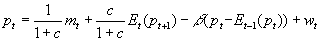 , where
, where 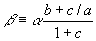 and
and  .
.
- How do you solve this system?
- Assume that all expectations are rational - i.e., with 0 mean error.
- Then, conjecture the form of the solution. It would make sense if the price level were a function of the money supply and the random shocks:
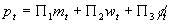 . Note that these coefficients are "undetermined": we don't yet know what they are.
. Note that these coefficients are "undetermined": we don't yet know what they are.
- (Note further that we assumed away trend growth; if there were trend growth, then presumably the price level would be a function of the money stock, random shocks, and the trends).
- Now, apply the expectations operator to the conjectured equation for pt:
- Lead the equation one period, plug in mt for Et(mt+1), and take the expectations at time t:
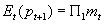 .
.
- Take the expectation of the equation at time (t-1), then substitute mt-j
t for mt-1:
 Then
Then 
- Substitute in for the expectations.
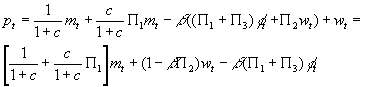
- Now notice: we have two equations for p as a function of m, w, and j
. So set the coefficients on both m's equal to each other, both w's coefficients equal to each other, and both j
's coefficients equal to each other.
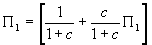 , so
, so 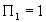 .
.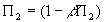 , so
, so 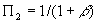 .
.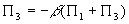 , so
, so 
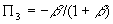
.
- The RE assumption has now led to a simple solution to this system of equations:
- For prices:
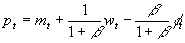 . The price level is directly proportional to the money supply, a positive function of investment shocks, a negative function of money demand shocks, and a negative function of unexpected money supply increases. (Note that increasing both m and j
by 1 still has a positive impact on prices, but less than proportional).
. The price level is directly proportional to the money supply, a positive function of investment shocks, a negative function of money demand shocks, and a negative function of unexpected money supply increases. (Note that increasing both m and j
by 1 still has a positive impact on prices, but less than proportional).
- Noting that
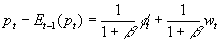 , the equation for output can also be derived:
, the equation for output can also be derived: 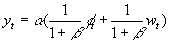
. Output is an increasing function not of money, but of unexpected money shocks; IS and LM shocks also have the standard impact.
- The New Keynesian Reply to RE (from Calvo)
- Simple RE models have stark implications:
- Anticipated monetary policy doesn't matter.
- Economies are always exceptionally at their optimum.
- Insofar as policy makes prediction more difficult, discretionary policy is itself a major cause of non-optimalities.
- This quickly sparked a "New Keynesian" reply, which broadly acknowledges #1, but disputes #2 and #3. 2 general approaches:
- Menu costs (e.g. Mankiw)
- Timing constraints (e.g. Calvo)
- In Calvo's model, firms are only able to change prices when "a random signal is 'lit-up.'" They may change their prices by however much they wish (including 0) while the signal is lit up.
- For mathematical simplicity more than anything else, the probability that you will be able to change your price today is independent of how long since you were last allowed to change your price.
- Consider the case of an individual price-setter with a fixed capacity. Assume further that you anticipate no changes in AD, and all other producers are producing at capacity. So long as your impact on the overall array of prices is negligible, you will want to set your price so that you too produce at full capacity.
- Suppose there is a sudden fall in AD, with no anticipated policy response. Suppose you are lucky enough to be allowed to change your price at once, before the other firms. What is your optimal response? Remember that eventually they too will be able to change their prices, reducing your demand at a given price.
- Suppose their is a sudden fall in AD. What can policy accomplish in spite of RE? What is policy still unable to do?
- Is this a sensible way to model nominal rigidity? Does it have any counter-intuitive implications?
- Why are Prices Sticky? (from Blinder)
- There are many theories of price rigidity, most of which are quite hard to distinguish just by looking at a scatter diagram or time series of prices and other macro variables.
- Blinder's strategy: why not just try asking businesspeople? While many deny that this is methodologically kosher, Blinder suggests that:
- When people have no incentive to lie, they will probably tell the truth.
- Translating jargon into plain English will get better responses.
- Other methods have problems too.
- Some precautions taken:
- Confidentiality promised.
- Originators of each theory of price stickiness asked to suggest improvements in question wording, and/or suggest additional testable implications. (Many did the former; none did the latter!)
- Sample is reasonably large, randomly selected, and representative of private, for-profit GDP. Only firms with sales over $10 M interviewed.
- Frequency results. (Interesting: 55% repriced no more than once per year).
- Shock-response results. (Typically around 3 month).
- "Race" results: the highest scorers are...
- Delivery lags (non-price adjustments)
- Coordination
- Cost-based pricing (suggests that wage rigidity may be causing price rigidity - wait till week 6)
- "Race" results: the lowest scorers are:
- Constant MC
- "Hierarchies"
- Judging quality by price
- Can you get any dissertation ideas out of Blinder's approach? There might be a GMU comparative advantage in this type of research...
- When Do RE Pay?
- Suppose that many people have disutility of being rational. Then the supply of rationality will be upward sloping: the more it pays to be rational in a given area of life, the more likely people are to be rational.
- Consider the following cases:
- Choosing religious or political beliefs.
- A worker thinking about his best response to a 1% increase in inflation.
- An employer thinking about his best response to a 1% increase in inflation.
- An arbitrageur thinking about his best response to a 1% increase in inflation.
- Important to distinguish between:
- Marginal gain from RE when everyone else has RE.
- Marginal gain from RE when no one else has RE.
- Where does this suggest RE is least likely to hold?
- Could the RE of some people make society act "as if" everyone had RE?
- Any anomalous cases, where benefits foregone are high, but people still don't have RE?
 .
.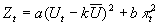 . Note k<1, so the policy-maker wants to push the unemployment rate below the natural rate.
. Note k<1, so the policy-maker wants to push the unemployment rate below the natural rate.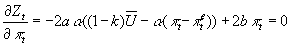
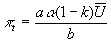 , yet
, yet 
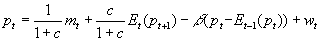 , where
, where 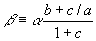 and
and  .
.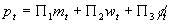 . Note that these coefficients are "undetermined": we don't yet know what they are.
. Note that these coefficients are "undetermined": we don't yet know what they are.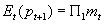 .
.  Then
Then 
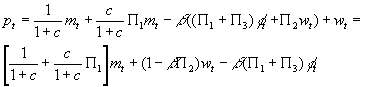
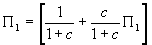 , so
, so 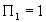 .
.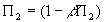 , so
, so 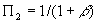 .
.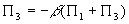 , so
, so 
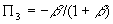
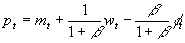 . The price level is directly proportional to the money supply, a positive function of investment shocks, a negative function of money demand shocks, and a negative function of unexpected money supply increases. (Note that increasing both m and j
by 1 still has a positive impact on prices, but less than proportional).
. The price level is directly proportional to the money supply, a positive function of investment shocks, a negative function of money demand shocks, and a negative function of unexpected money supply increases. (Note that increasing both m and j
by 1 still has a positive impact on prices, but less than proportional).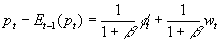 , the equation for output can also be derived:
, the equation for output can also be derived: