Prof. Bryan Caplan
bcaplan@gmu.edu
http://www3.gmu.edu/departments/economics/bcaplan
Econ 918
Spring, 1998
Week 7: Banking
- Bernanke's Questions About Banking
- Micro questions:
- What microeconomic function do banks serve?
- Why do banks combine short-term, liquid liabilities (e.g. deposits) and long-term, illiquid assets (e.g. loans).
- What causes bank runs and banking panics?
- Macro questions:
- Does banking instability (runs/panics) have macroeconomic costs?
- Are there macroeconomic justifications for regulating the banking system? If so, what form of regulation is needed?
- Is there a need for the central bank or other government institution to act as a "lender of the last resort" to the banking system? If so, how should it operate?
- These questions will be considered from three theoretical perspectives:
- Transactions cost theory of banking (Fama)
- Liquidity insurance theory (Diamond/Dybvig)
- Delegated monitoring theory (Calomiris/Kahn)
- Transactions Cost Theory of Banking
- Banks are just a special kind of low-risk, low-return mutual fund.
- Depositors receive fixed return, bank uses depositors' funds to buy assets. Assets have random return R, depositors get paid fixed return r, and on average (R-r) covers the transactions costs of running the bank.
- As in King/Plosser, there is no need for reserve requirements to create a determinate price level. It is merely necessary that someone (banks, the public, or both) wants to hold real base money. Just set the real money supply equal to this real money demand to find a determinate price level.
- N.B. Fama's spaceship analogy.
- Simple microanalytics of Fama:
- Computerization reduces banks' costs of completing each transaction.
- Massachusetts imposes taxes on (in-state) bank assets.
- People decide they like currency more.
- The government requires banks to hold non-interest-paying reserves with the central bank.
- The government requires banks to hold a minimum percentage of T-bills.
- A helicopter drops currency evenly over the economy.
- Fama and the micro questions:
- Banks are one form of mutual fund, presumably the one with the lowest cost of performing a certain range of financial services.
- No obvious answer, other than "that's the structure the customers want."
- Proximately, the customers' decision to re-arrange their portfolio. (Many factors could be responsible for this).
- Fama and macro questions
- No, although real macroeconomic problems could induce a run.
- No.
- No.
- Liquidity Insurance Theory of Banking (Diamond/Dybvig)
- Partial motivation: get a better explanation for the (mis?)-matching of liquid deposits and illiquid loans.
- Suppose there 3 periods (0, 1, 2), and two technologies:
- Investing in a long-term project; "planting" 1 unit of output now yields R>1 units of output two periods from now, but only 1 unit if project is "aborted" in period 1.
- Simple storage without deterioration.
- Also, consumers are ex ante identical; but in period 1 they learn their type (1 or 2). Fraction t is type 1; (1-t) is type 2. Consumers may learn that they need resources fast.
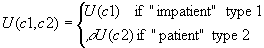
- Endowment in period 0 is 1.
- What happens under autarky? In period 0, each consumer gets
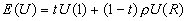 .
.
- But ex ante, this E(U) is Pareto-inferior to the "insured" equilibrium: maximize
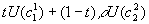 s.t.
s.t. 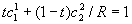 . Take partial derivative of E(U) wrt c1(1):
. Take partial derivative of E(U) wrt c1(1): 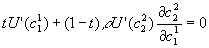 ;
; 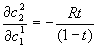 ; so
; so 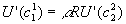 , which is different from the autarkic solution! (Need to assume risk-aversion and r
R>1). 1<c1<c2<R.
, which is different from the autarkic solution! (Need to assume risk-aversion and r
R>1). 1<c1<c2<R.
- So what do banks do? Banks feasibly implement the insured equilibrium.
- In period 0, everyone deposits in bank.
- In period 1, impatient people are allowed to withdraw 1<c1<c2<R.
- In period 2, patient people divide the remainder, getting 1<c1<c2<R.
- Problem #1: Incentive compatibility. People who know they are impatient will "buy insurance" they know they will use.
- Problem #2: If there is a shock to impatience, then the ex ante deal becomes infeasible.
- Suppose that normally, half are patient, half impatient, and R=2. Suppose the optimal insurance contract has c1=1.4, c2=1.6; this is feasible since 1.4*.5+1.6*.5=.5*1+.5*2.
- But if a shock raises the level of impatience to .6 happens, the patient people can't be paid off: 1.4*.6+1.6*.4=1.46, but .7*1+.3*2=1.3! So even the patient people would be better off demanding their "fair share" and then storing it one period, in order to get 1.46>1.3.
- DD and the micro questions:
- Banks allow the safe exploitation of productive, long-term projects.
- Banks use long-run investments because their return is greater; they use deposits to provide liquidity insurance.
- Unexpectedly high desire for liquidity (or even: "sunspot" expectation that there will be a high desire for liquidity).
- DD and macro questions
- Yes - it both reduces the chance to exploit long-run investments, and leaves individuals with more risk than under autarky.
- Yes - deposit insurance funded with lump-sum taxes can offset impact of high impatience.
- Yes - lender of last resort can substitute for deposit insurance.
- Puzzles:
- Why not make deposits variable instead of fixed? Eliminates runs, still allows long-term projects. With an equity cushion, this can still be low risk.
- Alternate perspective: Why do banks use a "sequential service constraint"?
- How well could "liquidity insurance" work given asymmetric info? Wouldn't customers just be sorted by risk, leaving little "insurance" function left? Note terms of CDs.
- Why couldn't insurance be taken care of in secondary markets?
- Delegated Monitoring Theory of Banking (Calomiris/Kahn)
- Partial motivations:
- Explain the existence of the sequential service constraint (SSC).
- Explain why bank runs historically targeted insolvent banks.
- Suppose there is 1 bank and 2 depositors.
- Each depositor has an endowment of 1. Depositors and banker are risk-neutral.
- 2 units of endowment can be invested by bank in technology with random return: get R2 (good return) w/probability g
, and R1 (bad return) w/probability (1-g
). The banker observes the return costlessly, but the depositors must pay information cost I in order to know which happened.
- Depositors can get outside safe return of S on 1 unit invested.
- Depositors can force liquidation midstream, yielding M=(1-L)R1.
- Banker may choose to "abscond" (metaphor for corruption, favoritism in loans, etc.) Absconding technology: if return is R, banker can abscond with (1-A)R. Otherwise pays contracted return P to depositors. (Why ever pay? If (1-A)R<R-P).
- Assumed to be more efficient to liquidate than abscond (L<A), and to abscond rather than pay return in bad state of the world (2S>AR1).
- Timing:
- Consumers decide whether or not to deposit.
- Consumers decide whether to buy info for I.
- Consumers decide whether to force liquidation.
- Banker decides whether to pay or abscond.
- Solving CK, Step 1: Is it worth having demand deposits (with right to gather info and order liquidation) at all? I.e., which has greater total surplus?
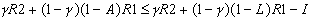 So DD is worth it when:
So DD is worth it when: 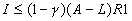
.
- Solving CK, Step 2: Figure out participation, incentive compatibility, and feasibility constraints on candidate equilibrium in which 1 depositor gathers info, and the other doesn't. This contract pays PNL if there is no liquidation; if there is a liquidation, the informed depositor gets PL1, and the uninformed gets PL2.
- Uninformed participation constraint:
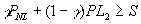 ; otherwise the uninformed depositor might as well just do the safe investment.
; otherwise the uninformed depositor might as well just do the safe investment.
- General incentive compatibility constraint:
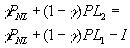 ; payoffs to both informed and uninformed must on net be the same.
; payoffs to both informed and uninformed must on net be the same.
- Uninformed incentive compatibility constraint:
-
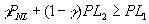
; otherwise might as well just announce "liquidate" in spite of lack of info.
- Informed participation constraint:

- Informed IC constraints:
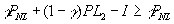 ; otherwise might as well not monitor and let banker abscond in bad periods (don't demand liquidation).
; otherwise might as well not monitor and let banker abscond in bad periods (don't demand liquidation).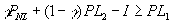 ; otherwise might as well not monitor and always demand liquidation.
; otherwise might as well not monitor and always demand liquidation.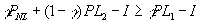
; otherwise, might as well monitor but LIE!
- Feasibility constraints:
- R2³
2PNL; good state>2 good payoffs
- (1-L)R1³
PL1+PL2; bad state>2 bad payoffs
- Solving CK, Step 3: Close model with banker maximizing profit s.t. outside return constraint.
- Then both uninformed and informed payoffs are exactly equal to S:
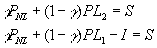
- Using substitution, note that
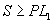 and
and 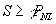 .
.
- So one obvious contract that satisfies ALL constraints sets:
- PL2=0
- PNL=S/g
- PL1=I/(1-g
)
- In short, an efficient contract enforces a sequential service constraint: the informed depositor gathers info, this inside info allowed him to see when the bank is shaky, and he withdraws his funds in full even in bad circumstances. Information costs are exactly balanced by information benefits.
- CK and the micro questions:
- Banks allow the safe exploitation of productive, long-term projects.
- Banks use long-run investments because their return is greater; they use deposits to provide incentives to monitor the bank.
- Bad states of the work cause bank runs; when investments flop, banks with bad loans go under.
- DD and macro questions
- No, so long as all runs are justified by bad info. But more advanced versions of this model (e.g. Chari/Jagannathan) yield some "sunspot" runs along with some information-based runs.
- No, unless the government has lower info costs than private institutions.
- No.
- Puzzles:
- Why are there system-wide bank runs? Is it just system-wide bad information? Or could there be some sort of information externality or coordination element, too?
- Bank Runs and Bank Insurance
- The three models yield quite different views of bank runs and bank insurance.
- Transactions cost: bank runs are harmless portfolio reallocations. Bank insurance is just a subsidy to risky investments. Bank insurance coupled with "safe asset" regulations lead depositors to reallocate wealth to unregulated sector to restore old risk/return composition.
- Liquidity insurance: bank runs are harmful, destructive events that damage long-term investment and create harmful wealth risk (via SSC). Bank insurance can eliminate runs. "Safe asset" regulations make it harder to undertake valuable investments, but also mitigate moral hazard problem.
- Delegated monitoring: bank runs mitigate the damage to the economy of bad investments; they reflect bad economic conditions, rather than constituting them. Deposit insurance short-circuits the beneficent monitoring incentive; asset regulations are heavy-handed replacements for private monitoring (by big depositors, presumably).
- System-wide runs have been worst in poorly diversified systems, often artificially created by regulations such as U.S. branch banking laws. Tends to support CK.
- Alternatives to Banking
- Why have banks at all? Why not have banks work like MMMFs and mutual funds - deposit values fluctuate with asset values?
- A simple transition:
- Announce that deposit insurance will be withdrawn in, say, 2 years.
- Further announce that deposit insurance will be withdrawn at once from banks that don't announce their intention to switch to fluctuating balances.
- Deregulate all other fluctuating financial accounts to make them checkable and allow ATM access, etc.
- My argument with White: There may be a taste for fixed balances, but if fixed-balance accounts are widespread there will be a severe time consistency problem: ex post, banks will be too likely to get bailed out.
- My reform is consistent with activist stabilization, but not individual bailouts. The Fed could still dump cash on financial markets if there is a liquidity crisis, but there would be no FDIC to insure individual accounts.
- Fluctuating balances can be very stable, as MMMFs indicate. So little loss of liquidity insurance caused by my reform.
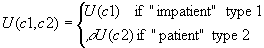
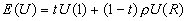 .
.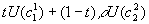 s.t.
s.t. 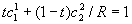 . Take partial derivative of E(U) wrt c1(1):
. Take partial derivative of E(U) wrt c1(1): 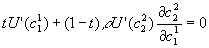 ;
; 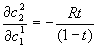 ; so
; so 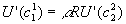 , which is different from the autarkic solution! (Need to assume risk-aversion and r
R>1). 1<c1<c2<R.
, which is different from the autarkic solution! (Need to assume risk-aversion and r
R>1). 1<c1<c2<R.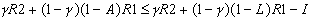 So DD is worth it when:
So DD is worth it when: 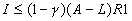
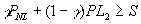 ; otherwise the uninformed depositor might as well just do the safe investment.
; otherwise the uninformed depositor might as well just do the safe investment.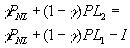 ; payoffs to both informed and uninformed must on net be the same.
; payoffs to both informed and uninformed must on net be the same.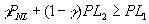

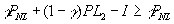 ; otherwise might as well not monitor and let banker abscond in bad periods (don't demand liquidation).
; otherwise might as well not monitor and let banker abscond in bad periods (don't demand liquidation).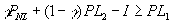 ; otherwise might as well not monitor and always demand liquidation.
; otherwise might as well not monitor and always demand liquidation.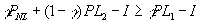
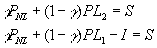
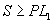 and
and 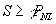 .
.