Week 8: Credit Market Imperfections + Exogenous Central Banking
- Questions About Credit Markets
- Why can’t you borrow as much as you want at the market interest rate?
- Why is repayment often so invariant to states of the world?
- Why do you need wealth to borrow money?
- Do credit market imperfections have important macro consequences?
- Simple Credit Market Imperfections: Moral Hazard and Adverse Selection
- Moral hazard: suppose there are two types of projects a borrower can invest in - safe and risky. The lender can’t distinguish the two, but the safe projects have probability/payoff (pa,Xa), and the risky ones have probability/payoff (pb,Xb), and paXa>pbXb even though Xb>Xa.
- If there is no payoff, then the borrower defaults; otherwise, the borrower repays the loan with interest. Expected repayment is therefore paR for a safe project, and pbR for a risky one.
- Therefore: there exists a critical R* such that if R>R*, borrowers choose the risky project instead of the safe one, and the bank’s return falls! To find R*: pa(Xa-R*)=pb(Xb-R*).
- Consider case where R>Xa.
- With a stock of loanable funds less than D(R*), there will be credit rationing. Either some people are randomly denied credit, or everyone is loaned less than they want to borrow at R*.
- How much can moral hazard really explain? Don’t banks require info on project riskiness?
- Adverse selection: Suppose there are two types of borrowers in the market: safe (q) and risky (1-q). The lender can’t distinguish the two, but the safe borrowers have probability/payoff (pa,Xa), and the risky ones have probability/payoff (pb,Xb), and paXa>pbXb even though Xb>Xa.
- So, if R>xa, only the risky types show up to borrow, whereas if R were less, both types would borrow. Expected return on $1 lent falls from R[q*pa+(1-q)pb] to Rpb.
- Optimal strategy: set R=xa.
- So again, if supply of loanable funds falls short of demand at R*, you ration instead of raising rates.
- Careful of corner solutions; note step diagram.
- How much can adverse selection really explain? Don’t banks require info on borrower riskiness?
- Advanced Credit Market Imperfections, I: Costly Monitoring (from Townsend)
- Principal and agent want to write a contract, such that the agent borrows from the principal, realizes a random return, and pays something back. The borrower observes the return directly, but the principal has to pay some information cost to "audit" the borrower/agent.
- Problem: Monitoring uses real resources. How can these be economized on without giving the borrower the incentive to lie?
- Short answer: Make payment fixed unless the borrower declares "default." If he does default, the lender monitors to find out the size of the total product, and takes it all.
- More rigorous answer: let R be the return to the project, distributed over [0, Rmax] with cdf F(R); r=safe interest rate; w=borrower’s endowment; b=(fixed) cost of audit; S=set of announced levels of R that induce audit; S’=complement of S; C is the no-audit repayment; g(R) is the payment (which can be negative) an audited party must make conditional on R.
- The borrower’s OF (note: risk-neutrality assumed) is to:
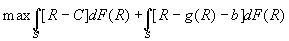
- The creditor determines the best values of C, S, and S’ subject to outside return and incentive compatibility constraints:
- Outside return:

- Incentive compatibility:
- C³
g(R)+b (for R in S)
- g(R)+b>C (for R in S’)
- Simplifying: If you sub (OR) into the borrower's problem, you get:
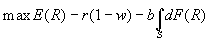 . This is equivalent to
. This is equivalent to 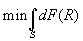 , s.t. the IC constraint.
, s.t. the IC constraint.
- Assuming that the default payment g(R) can't exceed R-b, what is the optimal contract?
- Incentive compatibility implies that the creditor has to monitor in the low states, and not monitor in the high states. Otherwise you could understate your earnings without penalty.
- You can reduce the range you monitor over by increasing the default payment as much as possible - so set g(R)=R-b whenever you monitor. (If lender didn’t do this, he could increase his earnings and leave the borrower indifferent by raising default payments and shrinking S).
- So: C marks boundary between S and S’; borrower pays C in S’, and gets audited and pays everything in S.
- Advanced Credit Market Imperfections, II: Limited Liability and Collateral
- Puzzle: You can get an even better contract if you allow default payments in excess of R-b. You can do so with a mixed strategy: with risk-neutrality, you can get the same deterrent effect from randomly inflicting a proportionally greater punishment. Alternately, why not simply raise the default payment up to g(R)=C so there is no incentive to default? Either way, you can reduce your monitoring costs to almost nothing.
- Resolution: there is a limited liability (or "feasibility") constraint. Creditors can’t take more than you have; you can declare bankruptcy; and human capital is inalienable in most modern legal systems.
- E.g., in the above example, the limited liability constraints could be:
- R³
g(R)+b (for R in S); R³
C (for R in S’).
- Then randomization or higher default payments could not improve the contract because you are already imposing as large a penalty as possible.
- Extension #1: Suppose a borrower has some collateral before he strikes a deal, and makes the offer to forfeit the collateral if he is unable to repay out of the returns on his project. Then the larger the borrower’s collateral, the larger the default penalty can be without violating the LL constraint, and therefore the smaller wasteful monitoring costs need to be.
- Extension #2: If business conditions affect the value of borrowers’ collateral, then worse economic conditions make credit market imperfections more severe, which could feed back into economic conditions.
- Consider: Fisher’s debt-deflation story.
- Example: Suppose a borrower with w<1 wants to invest in a project that requires 1 unit of resources. Thus, to do the project, the borrower must get (1-w) on loan; the safe interest rate is r. The payoff on the project is R=6 if the borrower exerts effort, and R=0 otherwise. Exerting effort requires a utility cost x, with x~U[0,10]; x is realized after the investment is made, but before effort is exerted. The borrower maximizes total return minus effort costs.
- What is the total surplus of socially optimal contract? It is socially optimal to exert effort whenever x£
6, so total surplus is:

- How does the social surplus depend on C, the required repayment? The borrower exerts effort only if x£
(6-C). This leaves social surplus
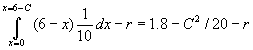 - a decreasing function of C!
- a decreasing function of C!
- What is the lender’s expected return as a function of C? Just
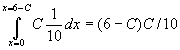 .
.
- What is the lender’s maximum expected return? Differentiate the above to find that it reaches a maximum at C=3, when expected return is 9/10.
- What does w*(r) look like, where w*(r) indicates the minimum amount of collateral a borrower must have for a loan to be offered? r(1-w*)=.9, so 1-w*=.9/r, implying that w*=1-.9/r. As r goes to infinity, w* goes to 1. Note that some projects with positive social value won’t be undertaken, e.g. if r=1.
- Macro Implications(?) of Credit Market Imperfections
- Are credit market implication severe micro problems? Are they severe macro problems?
- Moral hazard/adverse selection. Could these get worse during a downturn (or upturn)?
- Costly monitoring. Maybe costly monitoring adds to the initial burden of bad project results.
- Limited liability and collateral requirements. Probably the most plausible case of macro--> micro-->macro feedback. If money demand increases, the price level falls, reducing firms' credit-worthiness, leading banks to decrease loans in spite of lower velocity.
- Central Banking After Rational Expectations (but not Public Choice)
- Probably the main practical effect of RE was to diminish what people expected a central bank to be able to do.
- Pre-RE, central banks were often held accountable for low real output growth, high unemployment, etc.
- Post-RE, it is generally recognized that in the long-run money only changes nominal variables. The CB may matter for real variables in the short-run, but extended efforts to change real variables will typically just yield bad performance on both real and nominal variables.
- RE models gained prominence in macro around the same time that Public Choice theory became influential in public economics. RE questioned the ability of policy-makers to do things; Public Choice questioned their desire to do things; i.e., even if policy-makers could "succeed" in the public interest sense of the word, they might not want to.
- While the RE has become fairly influential in macro, the PC view of central bankers as self-interested bureaucrats has been far less so. The PC approach to money will be explored next week; for now, we will simply assume that CBs are open to (sound) exogenous policy prescriptions.
- What to Target
- The rules/discretion debate: anything more to be said? RE can be reconciled with either discretion or rules, but there is much more to say about rules than about discretion.
- N.B. The same policies may have different effects if one results from rules, the other from discretion. Constant money growth at the CBs discretion may work much worse than a constant money growth rule.
- N.B. Rules may have varying time horizons (the danger is that a rule with a very long time horizon is hard to distinguish from no rule at all).
- Interest rates - especially very short-run rates - are by far the most popular target of CBs.
- Advantages: Stabilizes interest-sensitive sectors; (?) easy for economic actors to understand; very easy to hit.
- Disadvantages: Indeterminancy problem - depending on level of inflationary expectations, the same nominal interest rate peg could be very expansionary or very contractionary.
- Money (variety of measures) - briefly popular target, but quickly de-emphasized.
- Advantages: (?) Transparency; determinacy; easy to hit.
- Disadvantages: Interest fluctuations; financial innovation requires re-definitions or growing irrelevance; velocity shocks.
- Inflation - growing popularity.
- Advantages: transparency; determinacy.
- Disadvantages: Requires contraction in face of negative supply shocks; not always easy to hit.
- Nominal GDP - theoretically dominates inflation-targeting, but less popular.
- Advantages: Determinacy; copes better with supply shocks than inflation targeting.
- Disadvantages: Opaque; probably difficult to hit.
- The Strategy of Monetary Policy (Bernanke/Mishkin)
- Case study of six CBs straddles exogenous and endogenous approaches. Partly describes what central banks do ("positive hypotheses"); partly tries to draw lessons about what policies work ("normative hypotheses").
- [Bernanke/Mishkin outline]
- Q#1: No CB strictly follows money growth or other rules. Is this (as Cbers would probably argue) for the best, or is there a PC or time consistency explanation?
- Q#2: Why don't all CBs copy the "successful" ones? Differences between countries' optimal policies? PC? Time consistency? Intelligence/ info costs?
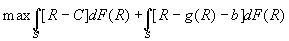

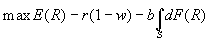 . This is equivalent to
. This is equivalent to 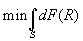 , s.t. the IC constraint.
, s.t. the IC constraint.
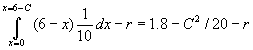 - a decreasing function of C!
- a decreasing function of C!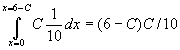 .
.