- Terminological note: "time consistent" is just what macroeconomists call "subgame perfect."
- First, assume policy-maker maximizes V, taking into account the impact of (unexpected) inflation on unemployment.
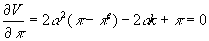
- Set expected inflation equal to actual inflation, since there are no random variables in this equation.
- But why do central bankers retain discretion? If the answer is something like: "To justify their existence" then this looks a lot more like a standard Public Choice view of bureaucracy.
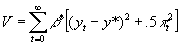
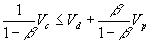
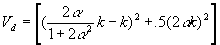
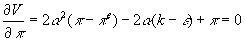 , so
, so