Prof. Bryan Caplan

http://www3.gmu.edu/departments/economics/bcaplan

Econ 918

Spring, 1998

1. Re-solve the simple RE model presented in class, with the following modifications:

a. Determine the impact of a money-targeting rule, so that .

If m_t is constant, then the money supply shocks all disappear. Therefore, using the results from the notes:

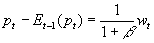and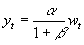

b. Determine the impact of an interest-rate targeting rule, so that .

i. Plug the constant value of i into the Fisher equation.

ii. Substitute the Fisher equation into the IS equation.

iii. Then conjecture . (Note also that: ).

iv. Plug this conjectured solution for money into the LM equation to get an equation for current prices, and take expectations of this equation to solve for the expectations terms.

v. Use all this info to solve for the implied values of , , and .

First, we need to solve for y_t. To do so, solve for p_t, getting . Then note that , and plug both equations into the AS equation:

Since shocks are transient, the expectation of the (t+1) price level in (t) is the same as the expectation of the price level in (t-1):

. Solving for y_t: .

-----

Moving along: plug the conjecture solutions for p_t and E_t(p_t+1) into (ii):

Then since ,

Collecting terms:

Now just figure out what the undetermined coefficients need to be so that the interest rate is constant - i.e., does NOT depend on the random shocks. Just put i on one side of the equation by itself, and figure out the implied values of m , P ₁, and P ₂. By inspection:

; ; . Thus, the implied money supply rule is:

, and . Notice that the answer still seems to be incomplete, since we want to substitute out for the m-bar terms. To do this, we merely need to specify the initial money stock m₀; then , , and .

In short, to raise the nominal interest rate by 1%, you need to permanently raise the expected rate of money growth by 1%. To actually hit the pegged rate, you have to adjust the rate of money growth on a period-by-period basis. But since shocks are transitory, your expected money supply in any period is independent of past shocks.