Prof. Bryan Caplan

bcaplan@gmu.edu

http://www3.gmu.edu/departments/economics/bcaplan

Econ 637

Spring, 1998

Weeks 1-2: Relationships Between Two Variables

  1. Is Econometrics Worthless?
    1. Econometrics has numerous detractors from a wide range of perspectives.
      1. The apriorists - Mises and Rothbard
      2. Broader Austrian critique
      3. Pure theorists generally
      4. (Some) econometric theorists
      5. (Some) economic historians
      6. Cynical empirical researchers generally
      7. Relativist philosophers of science
      8. Others (e.g. McCloskey)?
    2. Even if you are a Misesian apriorist, econometrics need not be totally rejected.
      1. Apriorists make some empirical assumptions (e.g. disutility of work); it might be similarly plausible to make the assumption e.g. that preferences are fairly stable over time.
      2. Since economic theory only gives qualitative answers, econometrics can supplement theory with quantitative estimates.
    3. The other complaints are less fundamental: there may be a lot of "data-mining" and "regression fishing," but that doesn't show that the honest use of econometrics is useless. (Although it makes it hard to rely on the econometric work of other people).
    4. Two of the better criticisms:
      1. Econometrics crowds out other empirical work, especially economic history.
      2. Empirically, econometrics hasn't added much to our knowledge. Economic theory and common sense empirical assumptions give more answers (and econometrics is often not believed until it is consistent with theory and common sense).
    5. Whatever your judgment, it is worth learning econometrics just to understand and communicate with other economists.
  2. Probability
    1. Where x is any event, . The probability of an event ranges between impossible and certain.
    2. Where X is the set of all possible events x, . The probability that some possible event or other occurs is certain.
    3. Independence: X and Y are independent iff P(X,Y)=P(X)P(Y).
    4. Conditional probability: P(X|Y)=P(X,Y)/P(Y).
    5. Sometimes we want to look at continuous probability densities rather than just discrete distributions. This essentially means replacing summations with integrals, e.g.:
    .
  3. Expected Values, Variance, and Standard Deviation
    1. E(X) is just the mean or "average" of a random variable X. Formally, . (For continuous distributions, ).
    2. Note: unless X is a constant.
    3. Var(X). SD(X) is equal to the square root of Var(X). Intuitively, both measure the "spread" of a distribution. If X is a constant, then both SD(X) and Var(X)=0.
    4. In practice, Var(X) is a pain to calculate using the above definition. Fortunately, there is extremely useful formula that permits ready calculation: .
    5. Summing N independent draws from a random variable X has a very interesting property: while the expectation of the average of N draws is simply E(X), the SD(average of N independent draws of X)=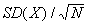
    . Intuitively, this means that the more independent draws, the more accurate the estimate of E(X) becomes.
  4. Covariance
    1. Covariance measures the linear association of two variables: if covariance between two variables is positive, the two variables are positively associated; if negative, then the two variables are negatively associated. If random variables are independent, then their covariance is zero.
    2. Cov(X,Y); slightly simpler formula: Cov(X,Y)=E(XY)-E(X)E(Y).
    3. Covariance ranges over the real numbers.
    4. Intuitively, imagine plotting some data, and then drawing a vertical line through E(X), and a horizontal line through E(Y). Points in quadrants I and III exhibit a positive association with each other; points in quadrants II and IV exhibit a negative association.
  5. The Correlation Coefficient
    1. Corr(X,Y). Thus the correlation coefficient always has the same sign as covariance. Correlation coefficient often written as r.
    2. Like covariance, it measures the linear association between two variables. The difference is that the correlation coefficient ranges between -1 and +1; making it much easier to interpret than covariance. (The unit of measurement drops out, so we know the r must be invariant to the method of measurement).
    3. If is high, then it is possible to make good predictions about one variable if you know the other.
    4. Proof that the correlation coefficient ranges between -1 and +1: for an arbitrary c, since the sum of positive numbers can't be negative. Then let ; plug this in for c to get . (This is known as the Cauchy-Schwartz inequality). Rearranging terms, it can be seen that r2£ 1, so -1£ r £ 1.
    5. Two problems with the correlation coefficient:
      1. Correlation isn't causation (much more later).
      2. Non-linear associations not picked up by r. (Can you think of a solution?)
  6. The Normal Distribution
    1. The so-called "normal" distribution will appear repeatedly throughout the course. Even the univariate normal has a quite complicated formula: , where s is the SD and m is the mean. This is often written N(m ,s ).
    2. The bivariate normal distribution has an even more complicated formula (eq.1.13 in DiNardo and Johnston). It contains five parameters: m x, s x, m y, s y, and r (the correlation coefficient between X and Y).
    3. The conditional variance of a bivariate normal is
    . This means that the conditional variance of Y does not depend on X; it is constant, aka "homoscedastic."
  7. The Bivariate Regression Equation
    1. Given a scatter of points, how can you "fit" a single equation to describe it? In particular, suppose you have 2 variables, X and Y. How do you "fit" the equation , where e is an "error term" that makes the equation true.
    2. Note: The text distinguishes between the
      "disturbance term" ui and the "error term" ei. You can think of the former as a random variable, and the latter as the observed realization of the random variable
    3. Let's make a few assumptions about ui. Note that since the e's are observed but the u's are random variables, what is true of the u's won't always be true of the e's. (For the same reason that the observed average roll of a die won't exactly equal exactly 3.5):
      1. ui is normally distributed.
      2. for all i (i.e., the expected disturbance equals 0)
      3. for all i (disturbances are homoscedastic)
      for all i¹ j (disturbances are uncorrelated with each other)
    4. In other words, we assume that the disturbance terms are normally distributed, iid (independently and identically distributed), with mean 0 and constant variance.
  8. Fitting the Bivariate Regression Equation to the Data
    1. With three or more points, it will normally be impossible to fit the data exactly. There will be a "error term" associated with each (X,Y) pair. It is possible to draw numerous lines through a bunch of points, but which is the "best" line describing the behavior of the data?
    2. General answer: minimize some function of the errors. Most common answer (which will be used throughout this class): minimize sum of squared errors. Aka "least-squares estimator."
    3. Step 1: Assume data fits some equation of general form: , where Y is the dependent variable, X is the independent variable, a and b are constants, and e is an error term that ensures that the equation is true.
    4. Step 2: Define SSE, the "sum of squared errors." (DiNardo and Johnston call it RSS, the sum of squared residuals).
    5. Step 3: minimize SSE, and solve for a and b. Then you will know what values of a and b minimize SSE given Y and X.
  9. Derivation of the Slope and Intercept Terms
    1. Standard minimization technique: take the partial derivatives wrt the variables you are minimizing over: , and set the equation equal to 0.
    3. Simplifying:
    4. Multiplying by 1/N and simplying, the first equation becomes: .
    5. Substitute value for a into second equation, to get:
    6. Solving for b:
    7. Useful formula:
    8. Now define . Then we have another, more convenient formula for b:
.
  1. R2 (or, Decomposition of the Sum of Squares)
    1. Note that . Then plugging in for b, it can be seen that . Therefore, .
    2. In words, this says that the total sum of squares TSS equals explained sum of squares ESS plus sum of squared errors SSE.
    3. Re-writing, it can be seen that R2=1-(SSE/TSS); note that R2 is simply the squared of the correlation coefficient.
    4. Consider some polar cases: when SSE=0; when SSE=TSS.
    5. This gives an interesting measure of how much of the variation in the data has been "explained." R2 ranges between 0 and 1 (this makes sense since r ranges between -1 and +1).
  2. Important Properties of The Simple Regression Model
    1. Property #1: Residuals sum to zero. ; plug in for a to get .
    2. Property #2: Actual and predicted values of Y have the same mean.
    3. Property #3: Least squares residuals are uncorrelated with the independent variable. Recall that if the correlation between two variables is zero, then the covariance between them is also zero. Then this may be proved using the following (and subbing in for b):
    4. Property #4: Predicted values of Y uncorrelated with least squares residual. Again, this will be proved by showing that the covariance =0.
  3. Coefficients and Standard Errors
    1. The bivariate regression yields estimates of both the constant, a, and a slope coefficient, b.
    2. But: we would also like to know how precise our estimates of a and b are. Statistically, we want to know the standard errors of the coefficients. For now, I'll just give you the answers; we'll derive it for k-variable regressions soon.
    3. Step 1: Estimate using .
    4. Step 2: Estimate var(a):.
    5. Step 3: Estimate var(b): .
    6. Step 4: To get from variances to SEs, take the square roots.
  4. Hypothesis Testing with Bivariate Regressions
    1. If were actually known rather than merely estimated, then our estimated coefficients would (under our maintained assumptions) be normally distributed around the true mean with SEs given by for a, and for b. Mathematically, .
    2. You could then construct confidence intervals for b with the help of a normal distribution table. For example, if you want to set up a 95% confidence interval, you find that the critical value is ± 1.96, so a 95% confidence interval for b is b± 1.96*. It is 95% likely that the true coefficient b lies in this interval.
    3. An hypothesis test is just the flip side of constructing a confidence interval. If your hypothesized coefficient value lies within a 95% CI, then you can "accept the hypothesis at the 5% level." If the hypothesized coefficient value lies outside the 95% CI, you can "reject the hypothesis at the 5% level."
    4. Complication: In practice, we have to estimate , so we can't use the normal distribution. Rather, we use the closely-related t-distribution. The t-distribution looks a lot like the normal distribution (becoming indistinguishable for large-N).
    5. The t-distribution depends on your number of observations (and your number of independent variables). As will be proven later, the "right" row to use for bivariate regression is (N-2), where N is your number of observations.
    6. Crucial difference: t-distribution has fatter tails, so your estimates are less precise. Suppose that you only have 5 observations; then to set up a 95% CI, go to the row for (5-2)=3 degrees of freedom. The critical value is 3.182, not 1.96 as it would be for the normal distribution. So a 95% CI for b would be b± 3.182*
.