Prof. Bryan Caplan

bcaplan@gmu.edu

http://www.bcaplan.com

Econ 849

Fall, 2001

 

I.                     Private Versus Social Benefits and Costs

A.                 Foundation of welfare economics: realization that private and social effects can differ.

B.                 Ex: A thief clearly enjoys private benefits of stealing.  But looking only at the thief's benefits misses the big picture: The thief making himself better off by making others worse off.

C.                Ex:  A person driving a polluting car is better off from driving, but that person isn't the only one who consumes the exhaust.

1.                  Contrast with: Worker safety trade-offs.

D.                How to measure "social benefits"?  The same way we always do: willingness to pay.  If some people benefit and some people suffer from a policy, the net social benefits are the SUM of the private benefits (positive and negative).

II.                   Negative Externalities

A.                 The basic idea of the tragedy of the commons is that when no one owns a resource, it gets over-used.

B.                 Question: But what exactly does "over-use" mean in economic terms?

C.                Answer: It means that there are costly side effects, or "negative externalities," that selfish agents don't factor into their decisions. 

D.                How do you diagram negative externalities?  In addition to the demand curve, draw a "social benefits curve."  With negative externalities, the social benefits curve will lie below the demand curve. 

E.                 Social optimum is at the intersection of the social benefits curve and the supply curve, but market equilibrium is at the intersection of the demand curve and the supply curve. 

F.                 If the social optimum differs from the market equilibrium, it is typically called a "market failure."

G.                Negative externalities are also often called "public bads," especially when the externalities are large relative to demand (so the socially optimal quantity is close to zero).

H.                 Ex: Pollution.  People value better air, but polluters normally have no incentive to care. 

I.                     The key: non-excludability.

1.                  There is no feasible way to exclude non-payers from the cleaner air.  

2.                  Since you do not have to pay to use it, selfish people will not pay to use it. 

3.                  And if no one will pay for it, why would selfish producers provide it?

III.                  Positive Externalities

A.                 Positive externalities are the other side of the coin.  Positive externalities are beneficial side effects that selfish agents don't factor into their decisions.

B.                 How to diagram?  Draw a social benefits curve above the demand curve. 

C.                Positive externalities are also often called "public goods," especially when the externalities are large relative to demand (so the equilibrium quantity is close to zero).

D.                Non-excludability is once again the key attribute.  If you can't exclude, there is no incentive to pay; if there is no incentive to pay, there is no incentive to produce.

E.                 Ex: Defense.  People value defense, but how can suppliers be paid to provide it?

VI.               The Irrelevance of Non-Rivalry

A.                 My definition of public goods and public bads departs from most textbook treatments - but, I would argue, not most actual applications.

B.                 Most textbooks focus on TWO attributes of public goods/bads, and treat either as a sufficient condition:

1.                  Non-excludability

2.                  Non-rivalry

C.                Non-rivalry essentially means any good with a MC of 0.  (Semi-rival, similarly, is MC<P).

D.                By this standard, though, all sorts of goods we routinely call private become "public."

1.                  Ex: Matinees at movie theaters

E.                 Failure of non-rival goods to be supplied for free is just another form of the monopoly problem.  There is no need to merge this with public goods theory.

F.                 Diagramming effects of non-rivalry versus non-excludability.  Non-rivalry is a distraction; non-excludability is the real problem.

VII.              Understanding Externalities

A.                 David Friedman's two caveats:

1.                  Must distinguish benefits from external benefits.  (E.g. education).

2.                  Must include both positive and negative externalities in your calculations.  (Important case: "pecuniary externalities").

B.                 Further insight from Friedman: "It is easy to misinterpret problems of market failure as unfairness rather than inefficiency... The problem with public goods is not that one person pays for what someone else gets but that nobody pays and nobody gets, even though the good is worth more that it would cost to produce." (p.278)

C.                Two common but controversial inferences from public goods theory:

1.                  Normative PGT: If something is a public good, government should provide it or subsidize it.  (And conversely, if something isn't a public good, then it shouldn't?)

2.                  Positive PGT:  Goods provided by governments are, at least in large part, public goods.  (And public goods are, at least in large part, provided by governments).

VIII.            Bad but Popular Examples; Good but Unpopular Examples

A.                 Some popular and plausible examples:

1.                  Air pollution

2.                  National defense

3.                  Highways and roads (especially local roads)

4.                  Law enforcement (especially victimless crimes)

B.                 Some popular but dubious examples:

1.                  Education

2.                  Health and safety

3.                  Fire

4.                  R&D...

C.                Some unpopular but plausible examples (depending on the society):

1.                  Censorship

2.                  Persecution of religious minorities...

IX.               Coase, Property Rights, and Externalities

A.                 Common sense ethics tells us to distinguish e.g. polluters from pollutees.  But from an economic point of view it can be equally efficient to make polluters pay pollutees for the right to pollute, or have pollutees pay the pollutees to pollute less.

B.                 Thus, as Coase argued, many externalities problems can be solved by defining property rights, then allowing parties to bargain.  So long as "transactions costs" are low, externalities won't be a problem.

C.                Corollary: eliminating property rights can turn any situation into a public goods problem.  (E.g. provision of food).

D.                Coase sheds new light on traditional problems.  Goods are rarely either perfectly exclusive or perfectly non-exclusive.  Rather, they are excludable at varying transactions costs.

E.                 Ex:  Why are local roads "more of a public good" than highways?  Transactions costs of toll collection.

F.                 Similarly, the "publicness" of R&D comes from transactions costs of exclusion.

X.                 Demsetz and Privatization

A.                 Demsetz used this transactions costs analysis to explain why there are property rights for some things but not others. 

B.                 Ex: You get private ownership of land when the transactions costs of exclusion get small enough relative to the value of land.

C.                Often, however, private ownership does not exist even though the transactions costs of having private property seem low. 

D.                The economic logic of privatization is to take advantage of these opportunities to transform public goods into private goods.

E.                 Two contrasting cases: commons versus state property.

1.                  Privatizing the commons is a particularly simple idea: create property rights so there is some incentive to produce and conserve.

2.                  Privatizing state property is more complex.  There the problem is often productive and allocative inefficiency due to bad incentives rather than non-existence due to lack of any incentives.

XI.               Fallacies of Group Action

A.                 Generalization of public goods theory: People often think in terms of groups acting to promote their group interests, just as individuals promote their self-interest.

1.                  Workers/capitalists

2.                  Women (and men?)

3.                  Environment

B.                 But this is a fallacy of composition.  Just because all members of group X would benefit if all members did something, it does not follow that it benefits any individual member to do so.

C.                Ex:  Suppose one worker decides to just stay home and watch TV while the other workers foment revolution.

1.                  Case 1: Revolution succeeds, all workers (supposedly) enjoy a brave new world - including the couch potato.

2.                  Case 2: Revolution fails, all workers continue to suffer under the capitalist system - but at least the couch potato got to watch some amusing television programming.

D.                We do need to be careful before we assert that there is no selfish reason to contribute.  Frequently there are "byproducts" and other "selective incentives" that make contribution selfishly optimal.

1.                  Ex: Trotsky on military discipline

XII.              Individual Impact: Probability and Magnitude

A.                 Saying that "The same thing will happen whatever you do" is admittedly an overstatement.  More precisely, "About the same thing will probably happen whatever you do." 

B.                 In other words, you have to look at the probability you make a difference and magnitude of that difference, then weigh it against the cost of acting.

C.                For example, it is possible that if you join the revolution, you will change the entire course of history.  Possible, but not likely!

D.                More relevant to public economics: the probability a vote matters and the magnitude of its impact.

E.                 Voting increases the probability that your favored candidates wins, but how much does it increase that probability? 

F.                 And even if your candidate does win as a result of your vote, how much will policy change? 

XIII.            Calculating the Probability of Decisiveness, I: Mathematics

A.                 When does a vote matter?  At least in most systems, it only matters if it "flips" the outcome of the election. 

B.                 This can only happen if the winner wins by a single vote.  In that case, each voter is "decisive"; if one person decided differently, the outcome would change.

C.                In all other cases, the voter is not decisive; the outcome would not change if one person decided differently.

D.                It is obvious that the probability of casting the decisive vote in a large electorate is extremely small.  Recent events in no way refute this.  Losing by 100 or 1000 votes is a long way from losing by 1 vote!

1.                  You might however say that Bush did win by a single vote on the Supreme Court!  But that is a voting body with only 9 voters.

E.                 There is a technical formula for "guesstimating" the probability of decisiveness using the binomial formula. (Brennan and Lomasky)

F.                 Suppose there are (2n+1) voters asked to vote for or against a policy.

1.                  Note: Assuming an odd number of voters avoids the picky problem of ties.

G.                Then the probability that YOU are the decisive voter is the probability that exactly n voters out of the 2n voters other than yourself vote "for."

H.                 Now suppose that everyone but yourself votes "for" with probability p - and "against" with probability (1-p).

I.                     Then using the binomial theorem:

J.                  From this formula, we can see that the probability of a tie falls when the number of voters goes up.  Why? 

1.                   gets smaller as n gets larger

2.                   is less or equal to 1.  When you raise a number less than 1 to a larger power, it must get smaller.

K.                 This formula also says that as the probability of voter support goes above or below .5, the probability of a tie falls.  Why?

1.                  When p=0, ; when p=1,  too.  In between p=0 and p=1, this term rises to a peak of  when p=.5, then falls.

L.                  Intuitively, the more lop-sided opinion on a topic is, the less likely there is to be a tie.  If everyone agrees, a tie is impossible.

XIV.          Calculating the Probability of Decisiveness, II: Examples

A.                 Let's work through some examples.  Remember that the number of voters is (2n+1), not n.

B.                 Example #1:  The close tenure vote.  n=10, p=.5. 

 

, or 17.8%.

 

C.                Example #2: The close county election.  n=5,000, p=.51.

 

, or a little more than 1-in-1000.

 

D.                Example #3:  The moderately close county election.  n=5000, p=.53.

, a little less than 1-in-8 billion.

E.                 Example #4: The moderately close state election. 

n=2,000,000, p=.51.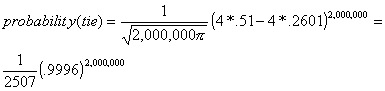 

a chance smaller than 1 in 10^-100!  (My calculator just says 0).

F.                 Upshot: For virtually any real-world election, the probability of casting the decisive vote is not just small; it is normally infinitesimal.  The extreme observation that "You will not affect the outcome of an election by voting" is true for all practical purposes.

XV.           Empirical Evidence on Collective Action Problems

A.                 One way to get a feel for the logic of collective action is to see how little participation in politics there is.  Survey of adult Americans from Dye and Zeigler:

Activity	%
Run for public office	<1
Active in parties and campaigns	4-5
Make campaign contribution	10
Wear button or bumper sticker	15
Write or call a public official	17-20
Belong to organization	30-33
Talk politics to others	30-35
Vote	30-55

B.                 Many experiments have been run to help improve our understanding of collective action problems. 

1.                  Part of the design: Rule out "selective incentives" accounts of apparently unselfish behavior.

C.                Standard design: 

1.                  I hand out a roll of 100 pennies to each person in the class. 

2.                  Then, people are allowed to secretly put any number of their pennies into a jar. 

3.                  You personally get to keep the pennies you don't put in the jar.

4.                  I count the number of pennies in the jar; then I distribute twice that many pennies to the class, with each person getting the same share.

D.                What maximizes the total income of the class?  100% donation by everyone!

E.                 What maximizes your private income (given 3 or more players)?  0% donation! 

F.                 The first couple of times you do an experiment like this, you typically get moderate to high levels of donation - 50-80%.

G.                Donation levels usually begin falling as you repeat the experiment with the same group.  After a while, donation levels often fall to around 20%.

1.                  For practical reasons, experiments usually only last a day or less.  So we can still speculate about what would happen if people played this game 10 times a day for a year.

H.                 Donation levels usually decline as the number of participants rises. 

I.                     The less secrecy there is, the higher the level of donation.

J.                  Conclusion: The "logic of collective action" appears to exaggerate the degree of human selfishness, but cooperation in these experiments is still far below the group-income-maximizing level.

XVI.          The Paradox of Public Good Provision

A.                 People often appeal to the "logic of collective action" to justify corrective government policy.  Public goods problems don't "solve themselves."

B.                 Problem: Isn't monitoring the government to act in socially beneficial ways itself a public good?

C.                Paradox: If citizens can voluntarily produce the public good of monitoring government, why can't they solve other public goods problems without government?  And if they can't voluntarily solve this problem, what reason is there to expect government to improve matters?