Prof. Bryan Caplan
bcaplan@gmu.edu
http://www3.gmu.edu/departments/economics/bcaplan
Econ 918
Spring, 1998
Week 6: The Optimal Rate of Inflation
- The Costs of Inflation and Inflation Volatility
- Many lump together the impact of inflation and inflation volatility. Since these are positively correlated, this is no surprise; but analytically, they are important to distinguish.
- Similarly, many lump together the redistributive and deadweight impact of inflation, counting both as "costs." These two should be analyzed separately.
- This generates four "boxes":
- Redistributive impact of inflation
- DW costs of inflation
- Redistributive impact of inflation volatility
- DW costs of inflation volatility
- Box #1: Redistributive impact of inflation.
- Government gets more inflation tax revenue.
- Non-government redistribution due to menu costs?
- Other?
- Box #2: DW costs of inflation.
- The tax on real cash balances. (With perfectly functional financial markets, this is just reflected in the nominal interest rate).
- "Shoe leather"/menu costs. (Although this is partly due to inflation volatility).
- Interaction between inflation and other tax distortions. (E.g. If nominal returns are taxed instead of real returns, then nominal taxes grow as inflation grows).
- Harm of inflation to productivity growth. (But is this due to volatility?)
- Other?
- Box #3: Redistributive impact of inflation volatility
- Non-government redistribution due to menu costs?
- Other?
- Box #4: DW impact of inflation volatility
- Losses due to imperfect insurance markets (taxes, credit markets, labor markets, etc.)
- Greater difficulty of long-term contracting.
- Menu costs?
- Productivity growth?
- Expectational errors get more severe - could lead to larger deviations from natural unemployment rate.
- Other costs emphasized by Leijonhufvud: diversion of resources to the inflation-guessing sector; political replacement of markets; multiple monetary standards; more?
- Other?
- The Case for Zero Inflation
- Why zero?
- Reduces inflation tax, but does not eliminate (unless nominal rates fall to 0 too).
- Substantial reduction in menu costs for goods. (But note: with increasing labor productivity, zero inflation can still entail big menu costs for labor).
- Question: Which is better from this perspective? Hitting zero on the un-quality-weighted inflation index, or zero on a Boskin-corrected inflation index?
- Reducing the deadweight costs of other parts of the tax code.
- Intertemporal allocation distorted by taxation of nominal interest.
- Capital stock distorted by taxation of nominal return.
- Housing stock distorted by deductibility of nominal mortgage interest payments.
- Feldstein's calculation: compare the one-time cost of disinflation with the PDV of the infinite-horizon benefits of disinflation.
- One-time cost: 5% of GDP
- PDV of benefits: 35% of GDP
- Why not just use indexation of capital income, or abolish capital taxes?
- The Case for Deflation
- Friedman's case for deflation: even zero inflation is probably too high, since nominal interest rates will remain positive, implying a positive tax on real balances.
- Can get the same result by simply paying interest on cash.
- Indeterminancy problems of zero nominal interest rate; same problems from payment of market rate of interest on cash.
- Selgin's productivity norm and deflation - a form of nominal GDP targeting.
- The case of the computer industry.
- Selgin's menu costs arguments:
- Need to consider menu costs for both final goods and inputs. Even e.g. with identical productivity changes for all final goods, zero inflation requires price adjustments for inputs. (Note that MVP=MPP*P).
- With unitary demand elasticity, and independent productivity changes in each industry, the zero inflation rule will generally require that all prices of both final goods and inputs change, while the productivity rule requires only changes of the prices of final goods.
- With elastic labor supply between industries, Okun's argument suggests that the unitary demand elasticity assumption is not needed.
- Expectational errors are less serious with the productivity rule, because each industry is better at predicting its own productivity gains than productivity gains in the whole economy (as they would need to with a zero-inflation rule).
- Selgin's supply-shock arguments:
- Positive productivity with zero inflation rule implies an expansionary response by central bank. While this stabilizes prices, it creates a labor market disturbance where none (may?) exist.
- Negative productivity shock implies contractionary central bank response. May create labor market disturbance where none exists (if workers demand inflationary adjustment for productivity shocks, this just compounds the problem).
- Selgin's arguments on creditor/debtor and indexation problems:
- Productivity norm provides better "insurance" than zero-inflation norm; zero-inflation requires same real repayment regardless of supply shocks.
- Note: Anticipated money will be reflected in ex ante rates, but would anticipated productivity shocks? Probably not.
- Note on Friedman's optimality rule: Productivity norm is closer to Friedman than zero inflation rule, but Friedman's rule actually requires deflation in excess of productivity growth.
- Some interesting historical examples:
- Depression of 1873-1896
- WWI
- The 20's
- Oil and agro shocks of the '70's
- Selgin's menu costs arguments support 0% nominal GDP growth, but other arguments would be consistent with higher nominal GDP target.
- Consider: Free banking on frozen fiat standard vs. commodity standard.
- The Case For Moderate Inflation, I: Evidence that Nominal Rigidity Exists
- Nominal wage rigidity (in levels) implies a long-run inflation/unemployment tradeoff may kick in at low inflation levels.
- Note: You could easily have productivity growth combined with flat nominal wages (MVP=MPP*P). But this won't necessarily work in industries with downwardly-inelastic demand, or if there are sectoral demand shocks.
- If long-run tradeoff exists, then Feldstein's PDV argument that the benefits of transition exceed the costs is much weaker.
- Bewley and Brainard: pay cuts rarely occur; pay freezes hurt morale much less than absolute cuts; pay cuts occurred only in exceptional circumstances (near bankruptcy, corporate takeover, "misalignment."
- Kahneman et al: Survey says that people consider pay cuts unfair except in exceptional circumstances. Irrationally different attitudes towards inflation-created real wage reductions. 62% said 7% cut with 0% inflation is unfair; 22% said 5% raise with 12% inflation is unfair.
- Campbell and Kamlani: Firms reluctant to cut wages because they lose "best workers," and damage productivity via morale. Also: white collar workers dislike nominal cuts even more than blue collar workers.
- BLS data shows skewed distribution: lots increase, some constant, almost no decreases. (S-s rule?)
- Same goes for Canada: with low inflation and high unemployment, a lot of people get no raise, but almost none get cuts.
- ADP survey: Just ask respondents if their wage changed; if their job had changed; and if their wage had gone up or down. Out of 409 who had not changed jobs, only 7 reported nominal cuts.
- Cuts from panel data stem from measurement error.
- The Case for Moderate Inflation, II: Akerlof, Dickens, and Perry Simulation
- Sets up model with monopolistic competition and heterogeneity of industries.
- Firm demand equation:
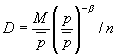 . D is the demand faced by one firm, M is the money supply, p-bar is the general price level, p is the price set by the firm, b
is demand elasticity, n is the number of firms.
. D is the demand faced by one firm, M is the money supply, p-bar is the general price level, p is the price set by the firm, b
is demand elasticity, n is the number of firms.
- Firm output proportional to labor: Q=L. Total labor force normalized to 1, u is unemployment, so Q=1-u.
- Bargaining equation: wage is weighted average of firm and worker surplus:
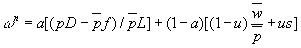 where omega-n is "bargained real notional wage per efficiency unit", w-bar is the average nominal wage, a is the index of worker bargaining power, s is the value of unemployed time, and f is the ratio of fixed costs to output value at full employment. Real wage is competitive when a=0.
where omega-n is "bargained real notional wage per efficiency unit", w-bar is the average nominal wage, a is the index of worker bargaining power, s is the value of unemployed time, and f is the ratio of fixed costs to output value at full employment. Real wage is competitive when a=0.
- This implies that price will be a constant markup over nominal unit labor cost:
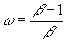 . (Implies acyclical wages and flat AD curve).
. (Implies acyclical wages and flat AD curve).
- From (3), one can derive the equilibrium AS curve by plugging in the equilibrium values:
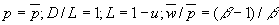 , so
, so 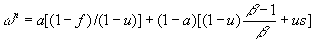 which will be upward-sloping so long as the value of leisure exceeds the real wage.
which will be upward-sloping so long as the value of leisure exceeds the real wage.
- Intersection of ADP AD/AS yields the LSRU ("lowest sustainable rate of unemployment") which is only identical to the NAIRU without nominal rigidity.
- Now add heterogeneity and rigidity.
- Add a random term to each firm's demand, and a random term to the bargaining equation. (Also build in autoregressive elements).
- Set up the simulation so that nominal wage cuts can only occur in extreme circumstances: firms with 2 years of consecutive losses can cut wages. Firms can get 1% cut per year via sneaky compensation cuts.
- Results (LSRU is 5.8%):
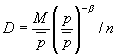 . D is the demand faced by one firm, M is the money supply, p-bar is the general price level, p is the price set by the firm, b
is demand elasticity, n is the number of firms.
. D is the demand faced by one firm, M is the money supply, p-bar is the general price level, p is the price set by the firm, b
is demand elasticity, n is the number of firms.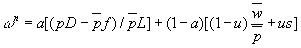 where omega-n is "bargained real notional wage per efficiency unit", w-bar is the average nominal wage, a is the index of worker bargaining power, s is the value of unemployed time, and f is the ratio of fixed costs to output value at full employment. Real wage is competitive when a=0.
where omega-n is "bargained real notional wage per efficiency unit", w-bar is the average nominal wage, a is the index of worker bargaining power, s is the value of unemployed time, and f is the ratio of fixed costs to output value at full employment. Real wage is competitive when a=0.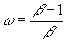 . (Implies acyclical wages and flat AD curve).
. (Implies acyclical wages and flat AD curve).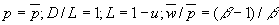 , so
, so 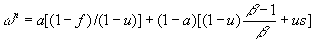 which will be upward-sloping so long as the value of leisure exceeds the real wage.
which will be upward-sloping so long as the value of leisure exceeds the real wage.